DESCARGAR PDF (incluye sexta, séptima y octava clase )
INTRODUCCIÓN
La probabilidad se presenta solamente en situaciones de incertidumbre cuando no existe la suficiente información para describir, decidir o emprender una acción. El estudio de la probabilidad es la base matemática de la estadística inferencial. Esta última funciona con muestras aleatorias, por lo tanto puede realizar sus cálculos con parte de los datos existentes. Esta situación ocurre de manera regular en el estudio de los fenómenos naturales y también en cuestiones relacionadas con la salud del ser humano.
Por lo general, en ciencias de la salud se realizan investigaciones con un cierto nivel de incertidumbre por lo tanto necesitamos entender las leyes de la probabilidad. Es importante saber a ciencia cierta cual es el nivel de incertidumbre implicada en nuestra investigación.
Según el problema el resultado es impredecible, por el grado de
incertidumbre debido a la falta de información. De esta misma forma en los trabajos de investigación debemos necesariamente tomar muestras aleatorias para
poder generalizar los resultados con un cierto nivel de confianza. Esto conlleva a un grado de incertidumbre propio del proceso. La incertidumbre, en los trabajos de investigación, es debido a que realizamos nuestros cálculos con una muestra aleatoria obtenida de la población, es decir trabajamos solo con parte de la información total.
La incertidumbre se puede cuantificar de modo que podemos saber cuál es el grado de certeza de lo que deseamos generalizar. Es decir qué tan confiable es el resultado que se obtiene. La incertidumbre es cuantificada por medio de un instrumento matemático denominado PROBABILIDAD.
La teoría de la probabilidad tiene como objetivo estudiar fenómenos o experimentos aleatorios en donde se haga necesaria la generalización de resultados a partir de datos Incompletos. De esta forma podemos decir que la probabilidad es la base matemática de la estadística inferencial.
Los fenómenos aleatorios tienen dos características importantes:
-Variabilidad
-Incertidumbre
Para cuantificar la variabilidad y la incertidumbre, de forma que sean controladas durante nuestra investigación se han creado modelos aleatorios que se ajustan en la mayor medida a la realidad del fenómeno estudiado.
Para cuantificar la variabilidad y la incertidumbre, de forma que sean controladas durante nuestra investigación se han creado modelos aleatorios que se ajustan en la mayor medida a la realidad del fenómeno estudiado.
Un experimento aleatorio es todo proceso que se puede repetir indefinidamente de la misma manera obteniéndose resultados imprevisibles. los resultados de un experimento aleatorio son en su mayoría diferentes aunque algunas veces se repiten.
ejemplo de un experimento aleatorio:
Lanzar una moneda no cargada sobre una superficie plana y observar la parte superior. En este experimento, el resultado puede presentarse de dos maneras: cara o sello. En otras palabras, se obtiene dos resultados posibles C ó S.
ejemplo de un experimento aleatorio:
Lanzar una moneda no cargada sobre una superficie plana y observar la parte superior. En este experimento, el resultado puede presentarse de dos maneras: cara o sello. En otras palabras, se obtiene dos resultados posibles C ó S.
Según el EJEMPLO 1 no sabemos, en principio si presentarán
síndrome del miembro fantasma una dos o tres personas o las diferentes
combinaciones que se pueden formar con tres sujetos, a esto es lo que
denominamos variabilidad. Ahora si
nos preguntamos cuál de ellas será o que grupo de dos o tres personas puede
presentar síndrome del miembro fantasma entonces estamos frente al hecho de la incertidumbre. La variabilidad responde
al hecho de las diferentes posibilidades en que se puede presentar un fenómeno,
mientras que la incertidumbre responde al hecho de cuál de las posibilidades es
la que presentará el fenómeno que estamos investigando. En este sentido la variabilidad es un presupuesto de la incertidumbre. Variabilidad es sinónimo de posibilidades e
incertidumbre es sinónimo del desconocimiento.
Existen algunos experimentos aleatorios que no se pueden repetir indefinidamente por ello existen dos corrientes en la estadística :
SUBJETIVISTAS: existen resultados que son imprevisibles y que no se
pueden repetir indefinidamente en los experimentos aleatorios. Por ejemplo: la vida y la muerte donde no se pueden repetir los hechos indefinidamente porque son
eventos únicos. También podríamos considerara el caso de la probabilidad de encontrara la cura para el SIDA o la probabilidad de que se origine la vida en un planeta en condiciones para albergar vida.
FRECUENTISTAS: hace el cálculo de la probabilidad empleando el uso de
las estadísticas.
Debemos considerar que hoy en día se hace uso tanto del enfoque
subjetivista como del enfoque frecuentista. Un ejemplo de ello sería el cálculo
de la tasa de mortalidad materna. Esta tasa es considerada una probabilidad de
muerte materna, y se trabaja con datos de hechos que ya han ocurrido. En el
terreno práctico esto nos sirve para elaborar las políticas de salud. Como
vemos en este problema de la mortalidad materna aplicamos los dos criterios de
la estadística.
En conclusión los experimentos aleatorios son aquellos que se pueden repetir
indefinidamente con salvedad de algunos casos que no se pueden repetir por su
propia naturaleza y que muestran resultados diferentes a pesar de que se realizaron bajo las mismas condiciones.
ESTUDIO MATEMÁTICO DE LA
PROBABILIDAD
La probabilidad tiene su nacimiento en los juegos de azar: dados y naipes. Al
conjunto de todos los posibles resultados de un experimento aleatorio se le
denomina espacio
muestral. Por ejemplo jugando al dado tenemos un conjunto de 6 posibles
resultados. El espacio muestral asociado al experimento aleatorio del dado es
(1,2,3,4,5 y 6) se le representa por la letra omega mayúscula.
Es muy importante definir bien el experimento que se va a realizar. En
el ejemplo del dado podemos variar considerablemente el conjunto de posibles
resultados(espacio muestral) solamente al considerar un doble juego
con el dado, de manera que la cantidad de posibles resultados aumenta y cambia
a un conjunto de pares ordenados, en total 36 pares ordenados. Si las condiciones del experimento aleatorio cambian el espacio muestral también cambia. La selección de los elementos que constituyen una muestra
debe realizarse sin repetición de manera que el espacio muestral sea el adecuado. Un EVENTO es cualquier subconjunto del espacio
muestral. Se le denota por letras mayúsculas latinas: A,B,C…
Para constituir un espacio muestral se debe tomar en cuenta dos requisitos:
1 A cada resultado del experimento le corresponde uno y
sólo un elemento del espacio muestral.
2 Cada elemento del espacio muestral representa un
resultado del
experimento.
ejemplos demostrativos elementales:
-Evaluar el estado nutricional de un niño menor de 5 años elegido al azar de una comunidad. Como resultado de esta evaluación, el niño puede ser clasificado en forma gruesa como “normal” (N) o “malnutrido” (M).
-Evaluar el estado nutricional de 3 niños menores de 5 años elegidos al azar de una comunidad. En esta situación, el experimento anterior se repite tres veces, y en cada repetición hay dos resultados posibles (N ó M) y el número total de repeticiones está dado por 2 X2 X2=8. Solamente hemos aplicado el principio de la multiplicación.
Al ejecutar el experimento se obtiene sólo uno de los siguientes
resultados:
(N,N,N);(N,N,M);(N,M,N);(M,N,N);(N,M,M);(M,N,M)(M,M,N)(M,M,M)
A partir de las condiciones enunciadas en el EJEMPLO 1 resolvamos ahora el ejemplo 2 mediante un diagrama de árbol:
S: tiene síndrome del miembro fantasma
N; no tiene síndrome del miembro fantasma
N; no tiene síndrome del miembro fantasma
ESPACIO MUESTRAL:
 |
| El espacio muestral cuenta con 8 eventos aleatorios que se calculan aplicando el principio de la multiplicación: 2x2x2=8 |
Con una persona adulta mayor solamente podemos tener dos posibles
resultados y para cada persona de este grupo de tres personas como vemos en los
gráficos.
El espacio muestral está conformado por 8 ternas
Recordemos que los eventos son los resultados que le interesan al
investigador.
Resultados:
Puede haber un evento que sea imposible para un experimento aleatorio como
en el caso de la pregunta D
Un ejemplo interesante:
Un fabricante de automóviles ofrece vehículos equipados
con accesorios opcionales. El pedido de
cada vehículo se hace: i) con o sin
transmisión automática, ii) Con o sin aire acondicionado, iii) con una
de tres opciones de un sistema estéreo, iv)
con uno de cuatro colores exteriores.
Ahora, determinemos el espacio muestral definido como el
conjunto de todos los tipos de vehículos
posibles. Para ello haremos uso de un
Diagrama de Árbol.
 |
| El espacio muestral cuenta con 48 eventos aleatorios que se calculan aplicando el principio de la multiplicación: 2x2x3x4=48 |
El espacio muestral es el evento que siempre ocurre sea cual sea el resultado
TIPOS DE ESPACIOS MUESTRALES
Los espacios muestrales pueden ser :
Finitos: podemos determinar el número posible de resultados
El ejemplo de arriba nos demuestra la existencia de espacios muestrales
finitos en este caso 30 posibles resultados.
Infinitos: no se puede determinar el numero posible de resultados
 |
| R.N: recién nacidos |
ÁLGEBRA DE EVENTOS
Algebra de eventos significa operación con eventos. Sabemos que el
espacio muestral es un grupo de posibles resultados de manera que
cada uno de estos posibles resultados es un evento. Podemos hacer un tratamiento
algebraico del espacio muestral considerándolo como un conjunto de eventos
donde cada evento es un elemento del conjunto o del espacio muestral. De esta
forma podemos aplicar los principios de los conjuntos.
Por ejemplo si tiramos y
lanzamos una moneda y un dado obtenemos un total de 12 posibles resultados. En
este caso un evento imposible sería obtener dos caras como resultados. O dos
seis. Otro ejemplo seria que en la facultad de medicina no puede haber un
estudiante de medicina humana y de tecnología médica a la vez. No olvidemos que
primero debemos definir el espacio muestral y luego los eventos
Este último caso se puede representar como la unión de tres eventos
mutuamente excluyentes:
Nos sirve para investigar en casos mutuamente excluyentes y complementar la
información.
Como vemos el álgebra de eventos se parece mucho al algebra de conjuntos
Propiedades de conjuntos que nos serán útiles :
Propiedades de conjuntos que nos serán útiles :
Definición de Complemento
(E´)´=E
Ley Distributiva
(A∪B)∩C=(A∩C)∪(B∩C)
(A∩B)∪C=(A∪C)∩(B∪C)
Ley Conmutativa
A∪B=B∪A A∩B=B∩A
Ley de Morgan
(A∪B)´=A´∩B´
(A∩B)´=A´∪B´
DEFINICIÓN CLÁSICA DE PROBABILIDAD
La definición clásica de probabilidad fue dada por el matemático Pierre-Simon Laplace y se aplica para espacios muestrales finitos y equi-probables. Lo cual
quiere decir que todas las posibilidades(cada evento) de un experimento aleatorio tienen la
misma probabilidad de ocurrir. Ejemplo de ello es el dado, cada una de las
posibilidades tiene un valor de 1/6.
La probabilidad de que ocurra un evento A: es el cociente entre el número
de resultados favorables para que ocurra el evento A entre el número de
resultados que tiene el experimento aleatorio.
La probabilidad de que nazca un varón es ½, es evidente que este evento
es equiprobable.
DEFINICIÓN DE PROBABILIDAD (JACOB BERNOULLI)
Por otro lado en un experimento donde debemos elegir una mujer de un grupo de estudiantes, en el que haya más mujeres que hombres, no podríamos aplicar la definición clásica de probabilidad, porque los eventos nunca serán equiprobables. Existe mayor probabilidad de ser elegida una mujer que un hombre. Es necesario decir que en este último caso se aplica la definición frecuentista de la estadística y para ello se emplean habitualmente cuadros estadísticos.
calculo de probabilidad:
Un hijo nacido de esta pareja y que tenga los ojos castaños tienen una probabilidad de ¾. No olvidemos que el espacio muestral está formado por cuatro posibilidades y que el evento “ojos castaños” es un subconjunto del espacio muestral que está constituido por tres posibilidades de cuatro.
PROBABILIDAD DE EVENTO NO ELEMENTAL
Para un espacio muestral discreto, la probabilidad de un evento E, denotada como P(E), es igual a la suma de las probabilidades de los resultados en E.
Ejemplo: La probabilidad de obtener al menos un 5 en dos lanzamientos consecutivos de un dado es de:
S2={ (1,1);(1,2);(1,3);(1,4);(1,5);(1,6)
(2,1);(2,2);(2,3);(2,4);(2,5);(2,6)
(3,1);(3,2);(3,3);(3,4);(3,5);(3,6)
(4,1);(4,2);(4,3);(4,4);(4,5);(4,6)
(5,1);(5,2);(5,3);(5,4);(5,5);(5,6)
(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
P(E)=1/36+1/36+1/36+1/36+1/36+1/36+1/36+1/36+1/36+1/36+1/36 P(E)=11(1/36)
P(E)=11/36
P(E)=0.306
La definición de probabilidad de Jacob Bernoulli se aplica cuando no
existe un espacio muestral equiprobable. En el ejemplo del salón con mayor cantidad de chicas, que vimos
anteriormente, podemos aplicar la definición para espacios muestrales no
equiprobable si observamos solamente el sexo de los alumnos en otros casos
podría aplicarse la definición clásica, como por ejemplo si solamente
observamos la condición de alumno en el salón.
En este tipo de experimentos en donde el espacio muestral no es
equiprobable se hace el uso de la frecuencia relativa, que como vimos en otro
capítulo es el cociente entre la frecuencia absoluta y el número total de
casos.
La probabilidad, haciendo uso de la frecuencia relativa, pone un límite a
la probabilidad de un evento. Se le denomina también ley de los grandes números. Este tipo de probabilidad se emplea generalmente para aproximar la
probabilidad de algún evento a partir de encuestas, censos o registros administrativos. Por
ejemplo la tasa de mortalidad materna sirve para aproximar o estimar una probabilidad.
La probabilidad de muerte materna se calcula como frecuencia relativa, es decir
el número total de madres fallecidas debido al embarazo entre el número total
de madres embarazadas, por ello si deseamos saber cual es la probabilidad de muerte materna para una gestante en un determinado hospital y en un determinado tiempo necesitaríamos saber cual es la tasa de mortalidad materna en un periodo anterior.
PAM: paciente adulto mayorRespuestas:
DEFINICIÓN AXIOMÁTICA
La definición la estableció el matemático ruso Andréi Kolmogórov .
Los axioma son:
Recordemos que la frecuencia relativa puede tomar valores entre cero y uno.
Para dos eventos mutuamente excluyentes la unión de estos dos eventos es la suma de los mismos.
La frecuencia relativa del espacio muestral es uno mientras que la frecuencia relativa del evento imposible es cero.
Otras propiedades:
Espacio muestral: recicladores de residuos sólidos de lima metropolitana.
Eventos:
-Recicladores con estrés P(A)=0.26
-Recicladores con dolor lumbar P(B)=0.31
-Recicladores con estrés o dolor lumbar
o ambos problemas P(AUB)=0.41
De los datos planteamos el problema del siguiente modo para la primera
pregunta:
En la primera pregunta nos piden la intersección entre el evento A y B
Como el evento A y el evento B no son eventos mutuamente excluyente
entonces podemos hacer uso de la propiedad 6:
Lo representamos mediante los diagramas de ven:
Para la segunda pregunta: nos están pidiendo solamente los casos de
individuos que pertenecen al
evento A pero no al evento B por lo tanto podemos aplicar:
Concluiremos que el álgebra de eventos nos sirve para que el investigador
pueda ganar información de los datos que tiene.
ENFOQUES DE LA PROBABILIDAD
SUBJETIVISTA: se aplica para eventos únicos y es propio de las personas.
Generalmente no se obtienen datos estadísticos. En estos casos se recurre a los
expertos que son conocedores de la ocurrencia de los eventos. Se aplica en los
seguros de vida, en la climatología y también en el campo médico para ciertas
enfermedades u operaciones donde el experto puede indicar la probabilidad
de supervivencia después de una operación. También vemos aplicaciones de este
enfoque en economía. Este tipo de eventos son predicciones porque
no existen cifras estadísticas de tales eventos. Es desventajoso en algunos
casos porque su tratamiento merita exclusivamente de un experto.
CLÁSICO (A PRIORI): Se le denomina a priori porque se pueden hacer deducciones a partir de ciertas condiciones mínimas ya que obedecen a la teoría debido a su carácter eminentemente deductivo. Se vale de axiomas preestablecidos. Se realiza perfectamente con la definición clásica de la
probabilidad. No es aplicable cuando se necesita investigar en grupos donde
existen frecuencias diferentes del evento que queremos estudiar por lo que están basados en la bibliografia. Es el enfoque más sencillo de todos, sin embargo se aplica diariamente en la practica. Se complica bastante cuando se presentan casos en los que existen eventos combinados.
FRECUENTISTA (A POSTERIORI): en este enfoque se consideran datos estadísticos. Se desarrolla en base a la
definición de probabilidad de Bernoulli. Es evidente que se trabaja con la
frecuencia relativa. Se dice que para eventos con gran cantidad de incidencias
o repeticiones la frecuencia relativa es el límite y establece por lo tanto la
probabilidad de que ocurra tal evento en un futuro. En otras palabras si algo ocurre
frecuentemente existe entonces una alta probabilidad de que pueda ocurrir
nuevamente. En las investigaciones en ciencias de la salud se aplica este enfoque con gran éxito. Se puede decir que, es el más usado en estadística. como vemos se denomina a posteriori porque a diferencia del enfoque clásico se necesita de datos extraídos de la realidad. por lo tanto se basa en una actividad empírica para deducir luego leyes y modelos de comportamiento.
Ley de regularidad de frecuencias relativas: la frecuencia relativa de un evento se acerca más y más a un valor fijo llamado probabilidad, conforme más veces se repite un experimento aleatorio, esto es:
Ley de regularidad de frecuencias relativas: la frecuencia relativa de un evento se acerca más y más a un valor fijo llamado probabilidad, conforme más veces se repite un experimento aleatorio, esto es:
A medida que los eventos son cada vez mayores en
cantidad estas se estabilizan sobre un valor probabilístico. Por ejemplo si
lanzamos una moneda la probabilidad de que salga cara es de un medio A PRIORI,
pero si utilizamos el enfoque frecuentista tendríamos que lanzar varias veces la
moneda de forma que a mayor cantidad de lanzamientos la frecuencia de que salga
cara ira hasta ser muy cercano a un
medio. El enfoque frecuentista hace uso de las
frecuencias relativas de eventos estadísticos, es decir que ocurren varias
veces. Mientras que en el enfoque a priori se hace una predicción sabiendo de
antemano las posibilidades de los resultados o sabiendo cual es el conjunto de
resultados ( espacio muestral)
Observamos como la
prevalencia se basa en el enfoque frecuentista
Por ejemplo dividimos el número de infectados el año pasado (500) entre el número total de la población en riesgo (6000)
La desventaja del enfoque frecuentista puede resultar inconveniente cuando
los datos son falsos, se registran mal, se pierde información o existe un gran sesgo en la recolección de los datos.
PROBABILIDAD CONDICIONADA
Ejemplo 10: en el EJEMPLO 7 si el reciclador elegido al azar:
1 tiene estrés,¿cuánto es
la probabilidad de que tenga dolor lumbar?
2 tiene dolor
lumbar,¿cuánto es la probabilidad de que tenga estrés?
Para la primera pregunta:
Estrés: A1
Dolor lumbar: A2
Para la segunda pregunta:
Estrés: A1
Dolor lumbar: A2
Dicho de otro modo:
La probabilidad de que
ocurra el evento A condicionado por el
evento B se denota por p (A/B) y se
define como el cociente entre la probabilidad de la intersección de ambos y la probabilidad de B.
Así:
Al lanzar un dado, la p(6)
= 1/6; pero, al lanzar un dado, la
probabilidad de que salga un seis, si se sabe
que (dado que, sabiendo que) ha salido un número par, es 1/3.
La probabilidad
condicional cumple las mismas
propiedades que la probabilidad de un evento:
La probabilidad condicionada significa que la ocurrencia de un evento está sujeto a otro evento. Se usa para hacer investigaciones, modelamientos y pronósticos.
Un ejemplo claro de la
aplicación de las probabilidades condicionadas se presenta cuando deseamos
saber cuál es la probabilidad de tener apendicitis, pancreatitis o colecistitis (evento A2)
cuando un paciente llega a un consultorio con dolor abdominal(evento A1). Otro
ejemplo seria: llega un niño desnutrido al consultorio médico y se quiere saber
cuál es la probabilidad de que el niño provenga de una familia pobre o de que
la madre tenga solamente nivel primario de instrucción.
Población de mujeres y
hombres según su frecuencia de fumar:
Se elige un sujeto al azar, cuál es la
probabilidad de que:
1 Fume siempre
2 Sea del sexo femenino
3 No fume y sea de sexo
masculino
4 Fume a veces o sea de
sexo femenino
Solución:
-Si del total
se selecciona un
sujeto al azar y
es
de sexo masculino, cual es la probabilidad de que siempre fume:
Interpretación:
La probabilidad de que la
persona seleccionada
siempre fume sabiendo que
es varón o dado que es varón es 0,2667
-Si del total se
selecciona un sujeto al azar , cuál es
la probabilidad de que fume a veces sabiendo
que es de sexo femenino?
-Si del total se
selecciona un sujeto al azar, cuál es la
probabilidad de que no fume dado que es
de sexo masculino?
SENSIBILIDAD Y ESPECIFICIDAD SON PROBABILIDADES CONDICIONADAS
Tanto la SENSIBILIDAD como la ESPECIFICIDAD son probabilidades condicionadas, en toda regla, veamos un ejemplo extraído del articulo "Probability in Radiology":
La probabilidad de
que una mujer seleccionada al azar tenga cáncer de mama no detectado
de al menos 1 cm de diámetro tiene un significado especial porque la probabilidad no es
la misma para todas las mujeres seleccionadas de forma aleatoria. Es más alto para las mujeres que
nunca se han sometido a un examen mamográfico, que para las mujeres que si se hayan realizado este procedimiento radiológico, en igualdad de condiciones. La probabilidad de que una mujer, que nunca
haya sido examinada tenga un tumor de este tipo se denomina probabilidad
"condicionada", porque se define como la probabilidad de que la mujer
tenga un tumor de 1 cm o más, dado que la mujer nunca ha sido examinada mediante mamografía. Al usar la sintaxis: Prob (A/ B) para
denotar la probabilidad condicional de A (una mujer con un tumor de mama de 1 cm o más) dado B (no se sometió a un examen de mamografía), tenemos:
Esto constituye la base de la definición de sensibilidad y especificidad. Si entendemos que A representa un resultado positivo del examen mamográfico y que B representa la presencia real de la enfermedad, entonces Prob (A / B) es la sensibilidad. Recordemos que la sensibilidad es la posibilidad de un resultado positivo entre individuos con enfermedad lo cual constituye un resultado positivo verdadero.
Esto constituye la base de la definición de sensibilidad y especificidad. Si entendemos que A representa un resultado positivo del examen mamográfico y que B representa la presencia real de la enfermedad, entonces Prob (A / B) es la sensibilidad. Recordemos que la sensibilidad es la posibilidad de un resultado positivo entre individuos con enfermedad lo cual constituye un resultado positivo verdadero.
También resulta similar en
el caso de dos pruebas diagnosticas que se realizan una después de otra para
corroborar un resultado positivo: si se requiere la confirmación de cualquier
resultado positivo de la prueba, D1+ por medio de un segundo resultado positivo
de la prueba, D2+, entonces la posibilidad de que obtengamos dos resultados
positivos de la prueba viene dada por la ley de probabilidades
“multiplicativa”: Prob (D1+ ∩ D2+) = Prob (D2+ / D1+) x Prob (D1+). Probability
in Radiology
INDEPENDENCIA DE EVENTOS
Dos
eventos pueden no tener ninguna relación entre si, entonces estamos hablando de
la independencia de eventos.
A y B son eventos independientes cuando ocurre lo siguiente:
- La probabilidad de A dado que ocurrió el evento B es igual a la probabilidad de A
- también podemos indicarlo del siguiente modo: si se cumple la siguiente ecuación entonces los eventos son mutuamente independientes.
Esto quiere decir que la probabilidad de
la ocurrencia simultánea de dos eventos es
igual al producto
de las probabilidades.
La elección de un candidato es un evento dependiente de otros eventos. Por otro lado la inteligencia y el sexo son dos eventos independientes.
Podemos demostrar si dos eventos son independientes de las dos
formas antes definidas.
- Por la primera forma:
A1 y A2 no son independientes
- Por la segunda forma:
A1: tiene estres
A2: tiene dolor lumbar
¿A1 y A2 son independientes?
A1 y A2 no son independientes
TEOREMA DE BAYES
Se utiliza cuando el
espacio muestral presenta particiónes. Una partición se da
cuando un espacio muestral está constituido por eventos mutuamente excluyentes.
Este teorema se aplica en
una situación en donde es posible conocer las probabilidades de que ocurra una
serie de eventos. Ai que tiene la
propiedad de formar una partición del espacio muestral, que se observa en el
siguiente gráfico:
El espacio muestral
particionado representado por el gráfico de arriba es "omega" y está constituido por diferentes eventos. A1, A2; …tiene en total k eventos.
Si reunimos todos los
eventos tendremos el espacio muestral:
En
el espacio muestral omega está ocurriendo un evento común denominado B cuya
ocurrencia proporciona cierta información. Las probabilidades de ocurrencia de
B son distintas según el evento Ai que haya ocurrido. Entonces conociendo que
ha ocurrido el evento B, el teorema de Bayes nos indica las probabilidades de
la ocurrencia de los eventos Ai condicionados o sujetos a que haya ocurrido el
evento B. La formula para el calculo de la probabilidad de un evento de omega
es la siguiente:
Esta formula también se puede expresar como:
Esta formula también se puede expresar como:
El evento: "partición
Ai" depende de el evento B. O dicho de otra manera la probabilidad de que
ocurra cualquiera de los eventos del espacio muestral omega depende de la
probabilidad de el evento común B
Un ejemplo de lo
anterior lo veríamos en la Facultad de Medicina de San Marcos (espacio
muestral). En este caso, las cinco
escuelas forman los diferentes eventos
de la partición. Un evento común entre estas cinco escuelas es por ejemplo la
pertenencia al quito superior de cualquier alumno de esta facultad. Los alumnos se encuentran estratificados por diferentes eventos (pertenecer
a una escuela) y el evento común es que pertenecen solamente al quinto
superior. Se elige al azar a uno de estos alumnos que tienen como evento en común
pertenecer al quinto superior. Se quiere saber cuánta es la probabilidad de que
este alumno pertenezca a la escuela de Tecnología Médica. En este caso es evidente que debemos aplicar el teorema de Bayes. La probabilidad de que el alumno del quinto superior elegido pertenezca ademas a la escuela de TM es necesariamente una probabilidad condicionada.
A4: alumno de tecnología
medica
B: quinto superior
Un requisito importante para calcular la probabilidad de que un alumno del quinto superior que haya sido elegido y que pertenezca a la escuela de TM es conocer la probabilidad de cada una de las escuelas, es decir cuáles son las probabilidades de cada una de las escuelas para tener un alumno en el quinto superior. Es posible utilizar en este caso el enfoque frecuentista. Es decir cuántos alumnos del cien por ciento del quinto superior pertenecen a la escuela de TM. Si sabemos cual es la probabilidad de que un alumno de Tecnología Médica pertenezca al quinto superior podremos saber cual es la probabilidad de que un alumno elegido al azar sea de T.M.
Un ejemplo interesante
para aplicar el teorema de Bayes en el tema de la salud seria el siguiente: se
quiere saber cuál es la probabilidad de que un niño con desnutrición pertenezca
a un determinado nivel socio-económico:
-muy pobre : A1
-pobre:A2
-medio:A3
-alto:A4
-muy alto:A5
Niño en desnutrición: B
(figura ovalada del gráfico)
La gráfica seria la
siguiente :
Deseamos hallar P(A3/B):
cuál es la probabilidad de que un niño con desnutrición pertenezca al nivel
medio económico
Según la definición de la
probabilidad condicionada:
Observamos que es
necesario tener la intersección entre el evento A3 (pertenecer al nivel medio)
y el evento B ( evento común).
De forma similar
calculamos P(B/A3) para poder obtener un equivalente de P(A3ᴖB)
De esta forma podemos
reemplazar en la formula anterior como se ve en el gráfico de abajo:
En el denominador ahora
deseamos tener la probabilidad total de "B" definida así porque posee zonas comunes con cada uno de los eventos
o de las particiones del espacio muestral. De esta forma la probabilidad de
"B" no es mas que la suma de las probabilidades que constituyen,en el
gráfico, el ovalo que representa la condición de estar desnutrido.
Para resolver este tipo de
problemas necesitamos conocer la probabilidad de cada uno de los cinco eventos
además de conocer la probabilidad de B dado (A1,A2,A3,A4 y A5). Generalmente
son datos del problema.
De lo anterior obtenemos
la fórmula del teorema de Bayes:
PAM: paciente adulto mayor
Espacio muestral: PAM
Cinco eventos:
A1: PAM independiente P(A1)=0.25
A2: PAM dependiente
leve P(A2)=0.30
A3: PAM dependiente
moderada P(A3)=0.15
A4: PAM dependiente
grave P(A4)=0.15
A5: PAM dependiente muy
grave P(A5)=0.15
Evento común: (B) viven
con su familia.
Probabilidades
condicionadas: ellas no deben sumar uno
P(B/A1)=0.15
P(B/A2)=0.10
P(B/A3)=0.08
P(B/A4)=0.20
P(B/A5)=0.20
La pregunta es : P(A1/B)
cuanto es la probabilidad de que las actividades básicas de su vida diaria sea
independiente.
Lo primero que debemos
calcular es la probabilidad total:
1 probabilidad total:
P(B)=P(A1)P(B/A1)+P(A2)P(B/A2)+P(A3)P(B/A3)+P(A4)P(B/A4)+P(A5)P(B/A)
P(B)=0.25 x 0.15+0.30 x
0.10 + 0.15 x 0.08 + 0.15 x 0.20 + 0.15 x 0.20
P(B)=0.151
2 aplicando el teorema de
Bayes:
P(A1/B)= 0.038/0.151=
0.251
EL VALOR PREDICTIVO POSITIVO
Y EL VALOR PREDICTIVO NEGATIVO SE OBTIENEN MEDIANTE EL TEOREMA DE BAYES
El VALOR PREDICTIVO POSITIVO (VPP) y el valor predictivo negativo(VPN) se fundamentan en el teorema de Bayes. En el articulo Probability in Radiology nos explican lo siguiente:
Si bien la sensibilidad y la
especificidad de una prueba diagnóstica son importantes no abordan por completo la cuestión de
preocupación del paciente después de que se haya realizado la prueba. Para el paciente, el
problema no es "¿Con qué frecuencia la prueba detecta una enfermedad
real?", Sino que, "Ahora que se conocen los resultados de la prueba,
¿cuál es la probabilidad de que tenga la enfermedad?" El paciente quiere
saber una probabilidad condicional que resulta ser inversa a la sensibilidad. Si
usamos Dx para denotar un hallazgo positivo y D para denotar la presencia real
de la enfermedad, el paciente no está tan preocupado por la sensibilidad, Prob
(Dx / D), como con el PPV: Prob (D/ Dx). La posibilidad de que haya enfermedad
presente dado que el resultado de la prueba fue positivo. Supongamos que tuviéramos
una prueba de diagnóstico utilizada para la detección cuya sensibilidad es del 95% (positiva en el 95% de todos los casos en los que la
enfermedad está presente) y una especificidad del 95% (negativa en el 95% de
todos los casos en que la enfermedad está ausente).Cuando la prevalencia de la
enfermedad es del 10%, de cada 10,000 exámenes de detección, podemos esperar
ver 1000 casos con un resultado positivo después de la prueba diagnostica. En lugar de pasar por el laborioso ejercicio de construir
tablas, la regla de Bayes nos da el PPV directamente. Para una prevalencia del
10%, Prob (D) = 0.10, tenemos PPV = (0.95 x 0.10) / (0.95 x 0.10) + (0.05 ×
0.90) = 0.095 / (0.095 + 0.045) = 0.679.
NOTA:
La regla de Bayes se aplica
a cualquiera de los dos eventos, A y B, no solo hallazgos positivos, DX y
presencia de enfermedad, D. La distinción entre el Prob (A / B) y el Prob (B /
A) también forma la base del Diferencia entre el análisis estadístico
convencional y bayesiano de un ensayo clínico. En el análisis estadístico
convencional de los resultados de un estudio, B representa la hipótesis nula.
Una vez realizado el estudio y observados los resultados A, la decisión
convencional sobre la verdad de B se basa en la probabilidad de A *, cualquier
resultado tan extremo o incluso más extremo que A, dado que B es cierto, Prob (
A * / B). Esta probabilidad se conoce como el valor de p. Cuanto menor sea la
probabilidad de que un resultado tan extremo como A, dado B, más fuerte será la
evidencia de que B no es cierto. Convencionalmente, algunos límites (conocidos
como el nivel de importancia) se establecen de antemano, y se considera que el
estudio tiene hallazgos significativos si el valor de P es menor que el límite.















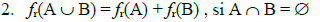








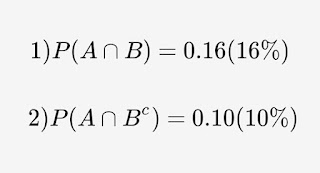

































No hay comentarios:
Publicar un comentario