TIPOS DE ESTADÍSTICAS
La estadística descriptiva es fundamental para el proceso de organización y resumen de
todo lo que se puede presentar como números. Sin una comprensión de los
conceptos clave que rodean el cálculo de estadísticas descriptivas, es difícil
entender cómo usar los datos para hacer comparaciones o sacar conclusiones(Radiology statistical concepts series-Seema S. Sonnad, PhD) .
ESTADÍSTICA DESCRIPTIVA
La estadística descriptiva resume y
presenta datos de las investigaciones descriptivas. El objetivo es caracterizar
los datos.
ESTADÍSTICA INFERENCIAL
La estadística inferencial trata del
estudio de las muestras aleatorias. Estudia su comportamiento. Los resultados
de este estudio sirve para la generalización de este comportamiento desde la
muestra a la población. Este tipo de estadística está basada en la
probabilidad.
ORGANIZACIÓN Y PRESENTACIÓN DE LOS DATOS
La claridad de dicha
presentación es de vital importancia para la comprensión de los resultados y la
interpretación de los mismos. Aunque se aconseja que la presentación de datos
numéricos se haga habitualmente por medio de tablas, en ocasiones un diagrama o
un gráfico pueden ayudarnos a representar de un modo más eficiente nuestros
datos (FISTERRA). En conclusión el análisis lo hacen las personas y el cálculo las máquinas.
Excel es una herramienta muy útil para elaborar bases de
datos. Un instrumento de medición puede ser un cuestionario impreso.
TABLAS Y GRÁFICOS DE DATOS DE VARIABLES CATEGÓRICAS O CUALITATIVAS (escala nominal y ordinal)
Las tablas y los gráficos de
frecuencias son una fuente de investigación por parte de las ciencias. Debemos
considerar que la actividad más importante durante el estudio estadístico es la
interpretación de la información que se muestra en la tabla o gráfico de
frecuencias. La interpretación de la información nos deja claro la relevancia del estudio
sobre alguna de las variables implicadas.
PROCEDIMIENTO
En las filas identificaremos a las unidades estadísticas y en las columnas a las variables en estudio(de identificación o contextuales), que pueden ser de la población o de la muestra.
Una data limpia es importante antes de empezar a obtener información y no caer en errores de estimación. Esta información se obtiene de la tabla de frecuencias.
La frecuencia evidencia las veces en que se repite en una población o muestra cada una de las categorías o niveles de una variable cualitativa. Por ejemplo cuantos sujetos pertenecen a una categoría. La frecuencia absoluta se refiere a la totalidad de una categoría. La frecuencia relativa es un cociente que se suele utilizar en términos porcentuales
TABLAS DE FRECUENCIA
En las tablas “K” es el número total de posibles valores que puede tomar la variable cualitativa. Para la tabla de frecuencias mostrada más arriba K sería igual a 6.
TABLAS DE FRECUENCIA
En las tablas “K” es el número total de posibles valores que puede tomar la variable cualitativa. Para la tabla de frecuencias mostrada más arriba K sería igual a 6.
La frecuencia
absoluta nos indica en número de veces que se repite cada posible valor
(categorías o niveles) por ejemplo la cantidad de individuos de sexo masculino.
A partir de la
frecuencia absoluta(por ejemplo masculino) se calcula la frecuencia relativa
que se obtienen de dividir la frecuencia absoluta entre el número total de
casos(hombres y mujeres).
La frecuencia
porcentual se obtiene de multiplicar la frecuencia relativa por cien.
Si sumamos todas
las frecuencias relativas el resultado es uno
Si sumamos todas
las frecuencias absolutas el resultado es el número total de casos.
Si sumamos todas
las frecuencias relativas porcentuales el resultado es 100 %.
El gráfico circular se utiliza para variables cualitativas o categóricas, es decir están medidas en la escala nominal u ordinal.
GRÁFICO DE FRECUENCIAS
Los gráficos de frecuencias cumplen con la misma función que la tabla de frecuencias. Para ello se hace uso de figuras geométricas.
El gráfico circular se utiliza para variables cualitativas o categóricas, es decir están medidas en la escala nominal u ordinal.
En el gráfico de frecuencias solamente se observa la información estadística no los datos.
En un gráfico circular cada categoría o nivel deben ser mutuamente excluyentes lo cual se indica con colores de alto contraste.
En un gráfico circular cada categoría o nivel deben ser mutuamente excluyentes lo cual se indica con colores de alto contraste.
En el gráfico de
frecuencias circular se empieza a representar las categorías a partir del
primer cuadrante y siguiendo el sentido de las agujas del reloj de mayor a menor frecuencia.
Si el número de categorías
es excesivamente grande, la imagen proporcionada por el gráfico de sectores no
es lo suficientemente clara y por lo tanto la situación ideal es cuando hay
alrededor de tres categorías(FISTERRA).
No olvidemos que
la leyenda de los gráficos de frecuencia deben colocarse en el mejor sitio
aunque no está normalizado. Las leyendas sirven para interpretar
correctamente el gráfico.
Nota: El gráfico de
barras ya no necesita leyendas.
Es importante en trabajos de investigación con fuente secundaria aclarar de donde proviene la tabla o gráfico estadístico y hacer el respectivo agradecimiento a la institución o persona que elaboró la información estadística.
En un trabajo de
investigación se pueden encontrar datos de:
Fuente primaria :
lo que el investigador genera
Fuente secundaria:
lo que el investigador cita o estudia e interpreta para su trabajo.
Cuando se hace el gráfico
de una variable categórica en Excel generalmente se copia esta en Word y se le
coloca el titulo por encima del gráfico, y por debajo la fuente de donde se
obtuvo el gráfico si este fuera el caso. No olvidar que el titulo puede tener
una llamada con un apostrofe que podrá leerse al pie del gráfico.
TABLAS Y GRÁFICOS DE DATOS DE VARIABLES CUANTITATIVAS DISCRETAS
Se dice que tenemos una
variable cuantitativa discreta cuando esta solamente toma valores enteros.
Estas variables se presentan en la escala de razón o intervalar.
PROCEDIMIENTOS
TABLA DE FRECUENCIAS
Para realizar una tabla de
frecuencias con una variable cuantitativa discreta se procede del siguiente
modo de manera manual:
Vemos en el gráfico de abajo
una tabla donde observamos en la primera columna el nombre de la variable
debajo de la cual se ubicaran las diferentes categorías de la variable. En la
primera fila observamos en primer lugar a la frecuencia absoluta y en seguida a
la frecuencia relativa.
Es muy importante TABULAR EL
RANGO DE LA VARIABLE antes de elaborar la tabla para saber si la tabla debe ser
hecha para contener en cada celda un posible valor de la variable en
estudio. Ello es así cuando los posibles
valores que puede tomar la variable son pocos como en el caso mostrado más
abajo.
Se calcula el rango de la
variable: “niños de 4 a 7 años” donde el rango es la diferencia entre el valor
máximo de la variable y el valor mínimo de la variable cuyo resultado es
3. Como tres es un valor bastante bajo
podemos tener la seguridad de que los valores que puede tomar la variable en
estudio son pocos. El numero de posibles valores que puede tomar la variable
es: el rango mas uno. Efectivamente los posibles valores que puede tomar la
variable(K) son 4 (4,5,6 y 7 años).
De manera que la tabla puede
ser hecha para contener todos los posibles valores. RANGO + 1= k
RANGO R = MAX(x)-MIN(x)
R= 7- 4
R= 3 (rango corto)
.
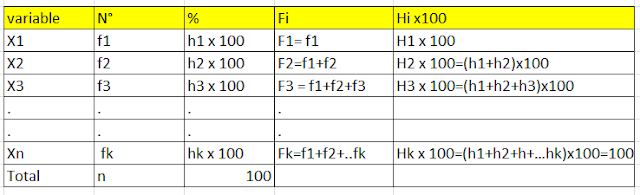
En la tabla que se muestra más
abajo observamos como los posibles valores de la variable han sido
ordenadas en forma ascendente( X1, X2,X3….Xk) donde k es el número de posibles
valores que toma la variable(numero de clases). En la columna inmediatamente a
la derecha observamos las frecuencias absolutas de cada uno de los posibles
valores de la variable( con el ejemplo anterior podríamos decir, en un supuesto
que un valor de la variable es 5 y que existen 34 niños de esta edad lo cual es
la frecuencia absoluta de un valor de la variable). Recordemos que la suma de
las frecuencias absolutas es siempre “n” (cantidad de unidades estadísticas)
Inmediatamente a la derecha observamos otra columna que nos indica los
porcentajes (resultado de multiplicar la frecuencia relativa por cien) de cada
uno de los valores de la variables. El resultado de sumar todos los porcentajes
siempre es el 100 %. Inmediatamente a la derecha de la columna de los
porcentajes observamos una columna en la que se encuentran las frecuencia
absolutas acumuladas para cada valor de la variable. Estas últimas son el
resultado de ir sumando progresivamente las frecuencias absolutas. Por ejemplo
para X1 la frecuencia absoluta acumulada
es solamente f1(primera clase), mientras que para X2 es f1+f2 (segunda
clase) y para X3 es f1+f2+f3 (tercera clase). También en el gráfico de abajo
también observamos inmediatamente a la derecha de la columna de las frecuencia
absolutas acumuladas la columna de la frecuencias relativas acumuladas para
cada clase. De manera similar al caso anterior cada clase resulta de sumar las
frecuencias relativas anteriores y multiplicar todo por cien como se observa en
el gráfico
La frecuencia relativa
acumulada también se puede calcular dividiendo la frecuencia absoluta acumulada
entre “n”.
Las frecuencias absolutas
acumuladas y las frecuencias relativas porcentuales solamente se calculan para
variables continuas discretas y continuas nunca para variables categóricas
porque no se pueden juntar clases mutuamente excluyentes.
GRÁFICA DE FRECUENCIAS
Para hacer el gráfico de una
variable cuantitativa discreta se emplea el eje de coordenadas. En el eje
horizontal siempre debe ir el nombre de la variable ( Se observa los valores
posibles que puede tomar la variable (X1,X2,X3….Xk). En el eje vertical siempre
irá las frecuencias absolutas o las relativas porcentuales.
El gráfico de arriba nos
muestra que para valores más altos la frecuencia es baja. No olvidemos que
siempre debemos poner el título del gráfico y su respectiva interpretación.
ejemplo:
Población: mujeres entre 19 y 29 años residentes en la ciudad de lima.
Muestra : 75 mujeres entrevistadas
Unidad estadística : una mujer
Variable: número de abortos que declaran haber tenido
Tipo de variable: cuantitativa discreta
Tabla :
1 hallemos el rango: valor máximo- valor mínimo : 3-0=3=R
de manera que los posibles valores que puede tomar la variable es de 4 posibles
valores (R+1). Rango corto
2 construcción de la matriz
3 en el tabla de arriba se puede evidenciar la población,
muestra, variable tiempo y espacio.
4 interpretación de la tabla:
1 ¿Cuántas mujeres
declaran haber tenido un aborto?
19
2 ¿Cuántas mujeres declaran haber tenido máximo 2 abortos?
66
3 ¿Qué porcentaje declaran haber tenido máximo un aborto?
69.33 %.
4 ¿Que porcentaje de mujeres declaran haber tenido 1 o 2 abortos?
44 %
Parte de la tabla que solamente
se utiliza para representar la frecuencia absoluta en Excel:
Gráfico:
Parte de la tabla que solamente se usa para representar gráficamente la
frecuencia relativa porcentual en Excel:
Gráfico:
El título del gráfico es
igual al título de la tabla. Los gráficos de este tipo de variables no ameritan
leyenda.
En el caso anterior la
interpretación global seria que la mayoría no ha tenido ningún aborto.
En el caso de que la
variable cuantitativa discreta posee una cantidad de valores posibles muy
grande se debe realizar los cálculos con
grupos .
TABLAS Y GRÁFICOS DE VARIABLES CUANTITATIVAS CONTINUAS
La escala de la variable
cuantitativa continua puede ser de razón
o intervalar y puede tomar cualquier valor. Por ejemplo si queremos determinar
alguna característica de los individuos de 6 a 26 años entonces nos encontramos
frente a una variable de tipo cuantitativa continua ya que entre 6 y 26 años
existen muchos valores posibles a pesar de que el rango es solamente R=20. Para
el caso de variables cuantitativas continuas los valores de la variable se toman en grupos
etarios, es decir, por intervalos de manera que en la gráfica ya no se verán
barras porque no existen espacios entre los intervalos.
Los intervalos pueden ser
cerrados (1) abiertos(1) o semi-abiertos(2). En total cuatro posibles
intervalos. El intervalo que emplearemos es el que está abierto por la derecha.
Lo primero que debemos hacer
como en el caso anterior es calcular el rango y si este es muy amplio debemos
seguir con el paso dos. Pero si el rango es corto trabajaremos como si fuera
una variable discreta. En la mayoría de casos de variables cuantitativas
continuas el rango será amplio.
Nota: Cuando el proceso de
construcción de algo es bastante controlado entonces el rango de variación de
alguna característica es muy pequeño. Esto puede suceder para algunas variables
continuas.
Continuando con el segundo,
debemos establecer el número de clases (K) o intervalos que deben tomar los
valores de la variable, el rango y el número de valores que puede tomar la
variable. Las clase pueden ser de cuatro a diez
por recomendación. Si el rango es muy amplio no conviene establecer
pocas clases pero si el rango es corto entonces no conviene establecer muchas
clases. El objetivo de esta parte del procedimiento es darle una presentación
adecuada a los datos. Si la presentación
de los datos ya tiene un formato establecido entonces debemos respetarlo.
Ejemplo de ello es el índice de masa corporal. Calculado el número de clases
determinaremos la amplitud de los intervalos de clase que se representa por la
letra C. que es igual al rango (amplitud de la variable) entre el número de
clases elegidas. En lo posible este cociente debe ser entero, y si no, podemos
redondearlo a un valor entero (siempre el entero mayor) pero modificando el
valor mínimo y el valor máximo de la variable.
Por ejemplo si el rango es
igual a 26 y el número de clases es 6 entonces la amplitud de clase real es de
4.33… lo que hacemos es redondearlo al valor entero más próximo y mayor que en
este caso es 5 (amplitud de clase modificada) de manera que el rango (amplitud
de la variable) también sufriría una modificación hasta un valor de 30 porque
la amplitud de clase modificada (5) por el número de clases es de 30. Este
último valor comparado con el rango real que es 26 es muy grande( existe una diferencia de 4 unidades
) por lo que buscamos un valor mucho más cercano de manera que consideramos el
valor de amplitud de clase modificada de 4.5 de manera que el rango modificado
es de 27. Este último valor solamente se diferencia en uno con respecto al
rango real por lo tanto es más factible trabajar con este valor.
No existe un modelo
matemático para establecer el número de clases porque ello depende del tipo de
variable, la cantidad de muestra y otros factores.
En cuento a los gráficos
puede emplearse:
1 EL HISTOGRAMA que representa a los intervalos de clase conjuntamente con sus frecuencias absolutas o relativas, simples o acumuladas.
2 EL POLIGONO DE FRECUENCIAS que emplean las
marcas de clase y sus respectivas frecuencias (absolutas o relativas)
Para ambos gráficos se
emplean el plano cartesiano. El eje horizontal está reservado para representar
a los datos (intervalos de clase o marcas de clase) de la variable y el eje
vertical representa a las frecuencias.
Observamos que el polígono
de frecuencias es cerrado para lo cual se usan los valores máximo y mínimo de
la variable reales o modificados. recordemos que la amplitud de la variable es
lo mismo que el rango de la variable. Mientras que la amplitud de clases o
amplitud de intervalo es el cociente entre la amplitud de la variable (rango) y
el número de clases.
Ejemplo:
Población: personas adultas mayores que han sido evaluadas en una
campaña municipal de salud en enero de 2015 en la ciudad de lima.
Muestra: 84 personas adultas mayores (enero 2015)
Unidad estadística: una persona adulta mayor
Variable: cantidad o nivel
de urea en sangre (mg/dl)
Escala de medición: de razón
Tipo de variable: cuantitativa continúa.
Tabla:
1 Rango: Vmax-Vmin=21-8.3=12.7 es un rango alto por lo que
utilizaremos intervalos.
La recomendación nos dice que debemos utilizar de 4 a 10
intervalos.
Por esta vez haremos varias tablas (con números de
intervalos o clases diferentes) para ver cuál es la más adecuada.
2 haremos tres tablas de 4,5 y 6 intervalos o clases.
k=4
Calculamos la amplitud de clase: C=12.7/4=3,175-----redondeado a 3.2
Rango modificado: 12.8: si se redondea la amplitud de
clase y se modifica el rango, como en este caso, entonces debemos modificar el
valor mínimo y máximo de la variable.
Si debemos modificar los valores mínimo y máximo de la
variable se hace de diferentes formas: sumando el valor de exceso al valor
máximo o quitándole este valor de exceso al valor mínimo, si el valor de exceso
es pequeño; pero si el valor en exceso es un poco grande podemos sumar un numero
al valor máximo y quitarle un número al valor mínimo.
En la tabla de abajo observamos que el primer valor del
primer intervalo es el valor mínimo (modificado o no) y el segundo valor
resulta de sumar el valor mínimo más la amplitud de clase modificada. Recordemos que este intervalo con valor
mínimo y máximo es de tipo abierto por la derecha, es decir, no toma el valor
de la derecha del intervalo.
Observamos también que el último valor del último
intervalo es el valor máximo modificado.
b: k=5
c: K=6 TABLA MAS ADECUADA PARA LA PRESENTACION DE LOS
DATOS
Como vemos no conviene
construir una tabla que acumule muchos valores en sus respectivos intervalos o
una tabla que considere muchos intervalos (especifica demasiado). El establecimiento del número de clases o intervalos es
producto de la experiencia y de la revisión bibliográfica, y como ya hemos
dicho depende mucho de la naturaleza de la variable. Cuando la
amplitud del intervalo es demasiado grande se puede estar mezclando información, si la amplitud del intervalo o de clase es más pequeña estamos
especificando demasiado e innecesariamente. No se debe fraccionar ni concentrar demasiado la
amplitud de la variable porque ello ocasionaría que se desvirtué la tabla y la
presentación de la información sea inadecuada. Observamos también que en la
primera tabla la mayor concentración de frecuencias se da en el tercer
intervalo mientras que en la segunda tabla se da en el cuarto intervalo y en el
tercero se da en el cuarto intervalo. Es importante observar que la tabla de 6
clases es la que nos ofrece la mayor cantidad de información observamos que la
mayor frecuencia se da en el medio de la tabla (intervalos 4 y 3). Por ello es
importante evaluar meticulosamente las diferentes tablas posibles.
Por lo tanto utilizaremos la
tabla de 6 casos para hacer la presentación de los datos.
Podemos hacer también la
tabla para frecuencias y porcentajes
acumulados aunque la presentación es solamente hasta frecuencias absolutas.
f2: 10 PAMS tienen de 10,3 a
menos de 12,5 mg/dl de urea en sangre
h3 x 100: 19,05 de las PAMS
tienen nivel urea en sangre igual a 13,6 mg/dl
F3:31 de las PAMS tienen un
nivel de urea en sangre de 8,1 a menos de 14,7 mg/dl
H4 x 100:73,80 % de las PAMS
tienen un nivel de urea en sangre menor o igual que 15,8 mg/dl
Recordemos que la marca de
clase (MC) es el valor que representa al intervalo. Observemos que en la última
pregunta se escribe menor o igual al promedio que es 15.5 porque esas es la
marca de clase para el porcentaje acumulado hasta el intervalo cuatro. Vemos
que podemos presentar los datos ( frecuencia absoluta, relativa o porcentual
acumulada ) respecto el intervalo o respecto la marca de clase.
Gráfico:
1Histograma
2 Polígono de
frecuencias : sabemos que este es un polígono cerrado para lo cual hacemos uso
del valor mínimo y máximo de la variable.
Interpretación de la tabla y del
gráfico: la mayoría de PAM
presenta valores de urea de 14.7 a menos de 16. 9 mg/dl que en porcentaje es
36.9 %. Los valores de urea tienden a adquirir valores centrales.
Comparación
de dos o más grupos
Cuando se quieren comparar
las observaciones tomadas en dos o más grupos de individuos una vez más el
método estadístico a utilizar, así como los gráficos apropiados para visualizar
esa relación, dependen del tipo de variables que estemos manejando. Por otro
lado, la comparación de variables continuas en dos o más grupos se realiza
habitualmente en términos de su valor medio, por medio del test t de Student,
análisis de la varianza o métodos no paramétricos equivalentes, y así se ha de
reflejar en el tipo de gráfico utilizado. En este caso resulta muy útil un
diagrama de barras de error (FISTERRA).
CONCLUSIONES
























No hay comentarios:
Publicar un comentario