DESCARGAR PDF
INTRODUCCIÓN
La estadística se divide en: estadística
descriptiva y en estadística inferencial. Hasta el momento hemos visto
solamente muchas de las cuestiones acerca de la estadística descriptiva como lo
son la representación gráfica y de frecuencias relativas de los valores de la
variable y luego las distribuciones de probabilidad entre ella la distribución
normal. Es precisamente esta ultima forma, de distribución la que nos ofrece un
modo de análisis y estudio de la probabilidad de los eventos de la variable
aleatoria, la que nos permite realizar con seguridad la inferencia estadística. Pasamos por lo tanto del modo descriptivo y exploratorio de los datos al modo
deductivo o inferencial en el que, en base a, los estadísticos podemos realizar
estimaciones acerca del verdadero fenómeno que acontece en la realidad.
La estadística nace de la falta de información y de un nivel de incertidumbre y variabilidad controlados, de manera que, asumiendo un riesgo de error aceptamos o rechazamos ciertas hipótesis formuladas durante la investigación científica, es decir, siguiendo el método científico.
La estadística nace de la falta de información y de un nivel de incertidumbre y variabilidad controlados, de manera que, asumiendo un riesgo de error aceptamos o rechazamos ciertas hipótesis formuladas durante la investigación científica, es decir, siguiendo el método científico.
TEORÍA
DEL MUESTREO
PROBABILÍSTICO
Para determinar una muestra antes debemos haber identificado el problema, que es equivalente a encontrar una linea de investigación. Luego debemos formular una pregunta de investigación y en seguida debemos determinar el diseño de investigación que depende del nivel de profundidad, exactitud en la investigación y de su factibilidad. Una vez establecidos estos pasos ya podemos determinar el tamaño de la muestra
En la estadística inferencial se realizan
estudios con muestras probabilísticas y con selección aleatoria. Debido a que en la estadística inferencial
se realizan estudios con muestras aleatorias
los resultados se puedan expandir o generalizar a toda la población bajo
estudio. El objetivo es conocer de esta forma el valor
del parámetro de la variable aleatoria o conjeturar acerca del valor del
parámetro, a lo cual denominamos hipótesis estadística. Por lo general se nos hace
imposible conocer el parámetro de una población debido a su dificultad. Por ello se puede estimar el valor del parámetro a partir de un estadístico
muestral asumiendo cierto valor de incertidumbre y por lo tanto de error.
La estadistica inferencial nos permite estimar el valor del parámetro
y esto se puede hacer de dos formas según el numero de variables implicadas:
- Estimación del parámetro mediante el
intervalo de confianza para estudios descriptivos
- prueba de hipótesis estadística para estudios analíticos
ELEMENTOS DE MUESTREO
POBLACIÓN:
“Colección completa de unidades (universo) del cual puede tomarse una muestra.”
Diccionario de epidemiología, 2008
-Las unidades comparten características
comunes y están delimitadas en: persona,
espacio y tiempo.
-Está presente en la pregunta de investigación.
MUESTRA:
“Subconjunto seleccionado de la población bajo estudio y cuyos datos
serán analizados.”
Diccionario de epidemiología, 2008
El objetivo es que tenga la misma relación "exposición-evento" que la población. La muestra debe tener las mismas características de la población de la que proviene. Logramos esta característica haciendo que la muestra sea aleatoria. Idealmente la muestra proviene de la población a la cual se quieren extrapolar los
resultados. Normalmente debe ocurrir así, aunque en algunos casos no es tan necesario que la muestra provenga de la población a la que se deben extrapolar los resultados.
Viabilidad: Tiempo y recursos. esta característica es la mas influyente en la determinación de la muestra. tiempo y recursos son dos limitaciones que en ultima instancia reducen la muestra hasta valores prácticos. Las pruebas estadísticas se basan en la variabilidad de la población y miden la probabilidad de haber seleccionado una muestra de esa población, a pesar de que a simple vista el estadístico se diferencie del parámetro.
La incertidumbre sigue siendo una propiedad estadística que forma parte del muestreo. El proceso por el cual tomamos una muestra aleatoria esta regido por el azar.
La incertidumbre sigue siendo una propiedad estadística que forma parte del muestreo. El proceso por el cual tomamos una muestra aleatoria esta regido por el azar.
TAMAÑO DE LA MUESTRA
Debe ser lo suficientemente grande para capturar la variabilidad
de la población y lo suficientemente pequeña para ser medible (factibilidad).
Depende del diseño y objetivo del estudio:
-Descriptivo vs.
Analítico: la muestra es diferente para un estudio descriptivo en el que solamente se busca estimar un parámetro, mientras que la muestra de un estudio analítico debe ser utilizado para relacionar o buscar una relación causa-efecto entre las muestras.
-Proporción vs.
Promedio: las muestras dependen del tipo de variable la proporción se calcula para variables categóricas mientras que el promedio es un parámetro o estadístico de una variable continua
veamos un caso típico de inferencia estadística:
Ejemplo 1:En un estudio sobre accidentes laborales, que ocurre en obreros de construcción civil, se desea conocer el porcentaje de accidentes laborales incapacitantes, que hay en el departamento de Lima.
Ejemplo 1:En un estudio sobre accidentes laborales, que ocurre en obreros de construcción civil, se desea conocer el porcentaje de accidentes laborales incapacitantes, que hay en el departamento de Lima.
Población: obreros del departamento de lima del año 2013
Variable: X= tiene accidente laboral incapacitante
Éxito:
sí
Fracaso:
no
-π: proporción poblacional de obreros de construcción
civil con accidentes laborales incapacitantes.
-se toma una muestra aleatoria de tamaño n para estimar
el valor de π
El circulo mayor en rosa representa a la población total de
obreros de construcción civil (universo), dentro de esta población se encuentra
otra población menor en la que todos sus elementos cumplen con la variable
estudiada, es decir personas que sufrieron accidentes laborales incapacitantes.
Esta población de obreros incapacitados por un accidente laboral se representa
por la letra π, que es toda la población
de obreros con esta característica. Sabemos en la práctica que por cuestiones
de logística y medios económicos no es posible estudiar a toda la población, por tal, debemos estudiarla por medio de una muestra aleatoria representativa. El circulo menor
representa a la muestra total formada por obreros con o sin accidentes
incapacitantes. De esta muestra separamos a los que sí han sido afectados por
la variable en estudio y es la que denominamos con la letra minúscula n.
Decimos entonces que π es el parámetro que nos interesa
estudiar, medir o cuantificar. También se dice que es el valor del parámetro
El estudio se realiza con la muestra aleatoria para conocer o estimar el valor del parámetro. Luego podemos tomar una decisión al respecto.
Un parámetro se define como el valor o la medida que va
a caracterizar a una población. Es un indicador estadístico poblacional que
da cuenta de la población en algún aspecto. Este valor del parámetro siempre
nos indica algo por ejemplo: bienestar, carencia, logro, necesidad de que se
establezcan campañas de salud, etc. Debemos indicar que el parámetro es teóricamente una
cantidad constante pero que en la práctica puede variar debido a que las
poblaciones se encuentran en constante cambio.
Si estamos midiendo una variable numérica trabajaremos con la media o la varianza poblacional y si estamos trabajando con
una variable categórica lo haremos con la proporción poblacional (π)
La contraparte del parámetro es el ESTADISTICO que por su misma naturaleza es una variable aleatoria y por lo tanto sus valores se obtienen a partir de una muestra
aleatoria(es lo más importante para el análisis estadístico)
Procederemos de este modo:
Si deseamos conocer o estimar la media, varianza o proporción
poblacional debemos conocer la media, varianza o proporción muestral.
Observemos que la varianza muestral es diferente a la
varianza que determinamos en estadística descriptiva. En esta última
calculábamos la varianza dividiendo entre n en la varianza muestral lo haremos
dividiendo entre n-1.
¿Cómo podemos saber que los estadísticos son los correctos y adecuados para saber el valor del parámetro?
Esto se hace claro y evidente por medio de la fundamentación matemática. Para
efectos prácticos debemos buscar la relación existente entre los valores de los
parámetros y los estadísticos.
CÁLCULO
DEL TAMAÑO DE MUESTRA
Se presentan diversas fórmulas que difieren solo en algunos factores. Las fórmulas son bastante parecidas y veremos que sus variaciones dependen del tipo de variable y del diseño de la investigación. La variable aleatoria puede ser cualitativa (también llamada categórica) o cuantitativa (también llamada numérica) y el diseño de investigación pueden ser descriptivo o analítico según en numero de variables que intervienen en el estudio. Tanto la naturaleza de la variable y el tipo de estudio determinan el tamaño de la muestra como veremos a continuación.
ESTUDIO DESCRIPTIVO
Los estudios descriptivos consideran una sola variable, nos encontramos dentro del caso UNIVARIADO. En este tipo de estudio deseamos estimar el valor de un parámetro a partir de una muestra. Pueden presentarse estudios descriptivos en los que se busque obtener el promedio muestral (para variables numéricas) o se busque saber cuál es la proporción muestral (para variables categóricas) de un grupo estudiado dentro de una población.
PROMEDIO
 |
| Esta fórmula es aplicable cuando no se conoce el tamaño de la población o su tamaño es infinita(sin marco muestral) |
La fórmula que mostramos arriba pone en evidencia cuales son los factores matemáticos que intervienen en el cálculo de la muestra. La varianza por ejemplo es propia de la población, mientras que el nivel de confianza está predeterminado y existe un consenso en su valor más adecuado. El margen de error influye directamente en el tamaño de la muestra ya que a menor margen de error la muestra será más grande. Dicho de otra forma si el margen de error es considerablemente pequeño necesitaremos una muestra considerablemente grande, que muchas veces es imposible obtener.
 |
| Se muestra la fórmula para el caso en que se conozca la población (población finita) |
VARIABILIDAD Y TAMAÑO DE LA MUESTRA
Si observamos la imagen de la izquierda fácilmente veremos que se trata de una población bastante homogénea al menos en lo que respecta a la edad de los individuos. Si midiéramos la varianza de esta población seria probablemente mínima. Por el contrario la imagen de la derecha nos hace pensar en una población con una altísima varianza al menos en cuanto a la edad de los asistentes al circo. Ahora pensemos en tomar una muestra del primer caso, los niños en la escuela. La muestra que debemos tomar en la escuela puede ser reducida ya que a pesar de que tomemos muestras muy grandes no se observaran diferencias muy importantes, basta con tomar una muestra reducida para acercarnos con seguridad al parámetro poblacional. En cambio la muestra de la población asistente al circo debe ser considerable ya que se trata de una población bastante heterogénea y por lo tanto de gran variabilidad. Por ejemplo, si seleccionáramos una muestra de tres personas asistentes al circo y resultara que estas tres personas eran padres de familia, entonces la muestra nos haría pensar equivocadamente en que la población del circo es la de personas de mediana edad . En este caso, la muestra no permitió incluir en nuestros cálculos la edad de los asistentes de menor edad, la de los niños asistentes al circo. Esto quiere decir que el tamaño de la muestra depende de la varianza poblacional. Una población de gran variabilidad amerita muestras muy grandes para poder acercarnos al parámetro poblacional en la mayor medida. El conocimiento de la varianza de una población es muy importante antes de determinar el tamaño de la muestra. La varianza poblacional se determina en base a la bibliografía sobre el tema que estemos investigando. Debe ser un dato establecido de antemano para nuestro estudio. La variaza poblacional da cuenta de la variabilidad de una población, y esta depende de su propia naturaleza o del estado en que se encuentre en un tiempo y en un espacio. Es muy importante conocer la población de la cual estamos extrayendo una muestra aleatoria antes de realizar cualquier investigación científica.
MARGEN DE ERROR Y TAMAÑO DE MUESTRA
El tamaño de la muestra depende en mayor medida del margen de error que estemos dispuestos a aceptar para nuestro estudio. La varianza y el nivel de confianza son dos variables matemáticas del calculo del tamaño de la muestra que no podemos controlar debido a que ya se encuentran establecidos desde antes del calculo de la muestra. Un margen de error reducido necesita de una muestra grande. Muchas veces no es posible obtener muestras considerables debido a las limitaciones y nos vemos obligados a permitir un margen de error relativamente grande, pero que no afecte tanto al valor y utilidad de nuestra investigación.
El margen de error da cuenta de que tan lejos nos encontramos de el parámetro poblacional cuando damos a conocer un estadístico. Es evidente que para lograr un 100 % de precisión en el estudio tendríamos que medir el parámetro en toda la población, lo cual no es práctico desde el punto de vista estadístico. Esto quiere decir que a medida que la muestra es más grande la precisión también lo es y el margen de error será más reducido.
Pongamos por ejemplo la siguiente situación, bastante sencilla y demostrativa:
Imagine que estamos en verano, y usted es "El hombre del tiempo" de un canal de televisión X. Es necesario, como es evidente, hacer una predicción del tiempo para el fin de semana. En base a la temperatura promedio alcanzada en los últimos días (26 °C) es posible hacer este tipo de predicción, y por lo tanto, decide que la temperatura que se alcanzará para este fin de semana será de 26 °C con un margen de error de +- 2 °C. Sin embargo, y como suele ocurrir, la temperatura del fin de semana fue de 29, un fin de semana bastante caluroso. Aunque no haya acertado en tal fenómeno meteorológico, la gente no tuvo mayores problemas, ya que la temperatura considerada por todos fue entre 24-28 °C y Todos usaron ese fin de semana una ropa bastante ligera porque no habría motivos para abrigarse demasiado. Pero usted no está dispuesto a equivocarse la próxima vez. Probablemente para el próximo fin de semana se animaría a realizar un pronostico con un margen de error más amplio, digamos que 26 °C +- 10, lo cual quiere decir que la población debería considerar una temperatura ambiente de entre 16°C y 36°C. En estas condiciones decimos que el margen de error dado es bastante amplio. Algunas personas, basadas en su pronostico no sabrán si abrigarse, considerando las temperaturas menores a 20 °C o si "introducirse en una congelador" considerando las temperaturas superiores a 30 °C.
Interpretemos ahora lo que sucedió en este caso: debido al afán de no equivocarse se amplio demasiado el margen de error lo cual disminuyo considerablemente la utilidad del pronostico. Cuando la población, debió considerar la posibilidad de temperaturas de entre 16-36 °C no supo que decisión tomar al respecto. Mientras más amplio sea el margen de error la utilidad de nuestro estadístico será menor. Cuando exageramos demasiado en la precisión (error máximo permitido) del estudio puede que la utilidad aportada sea mínima y no tenga una repercusión importante en la decisión que se deba tomar. Lo mejor es considerar un margen de error adecuado ni muy pequeño de forma que tengamos una muestra demasiado amplia y con una mejora mínima, ni muy grande de forma que la utilidad de nuestro estudio sea inservible.
El margen de error dependerá entonces de la factibilidad de conseguir muestras grandes, de la utilidad del incremento en la muestra y por lo tanto en la precisión lograda con un determinado aumento de precisión al reducir el margen de error. También dependerá de el tipo de variable bajo estudio y del tipo de estudio, analíticos descriptivo etc.
PROPORCIÓN
 |
| Esta fórmula es aplicable cuando no se conoce el tamaño de la población o su tamaño es infinita(sin marco muestral) |
Parámetros necesarios:
Z: nivel de confianza
p*(100-p): variabilidad de la proporción p (en porcentajes, generalmente son prevalencias) este factor normalmente proviene de la bibliografía.
∆:margen de error de la proporción(usualmente menor al 10%)
Observamos que la formula es bastante parecida a la formula para el cálculo del tamaño de la muestra en un estudio descriptivo sobre el que se esté estudiando el promedio de alguna variable. En realidad todas las formulas para calcular el tamaño de muestra se parecen bastante o son casi idénticas sin importar el tipo de variable(cuantitativa o categórica) o el tipo de estudio (descriptivo o analítico).
Para el calculo del tamaño de muestra en un estudio descriptivo y de una variable categórica (calculo de una proporción) la diferencia se presenta en: "p*(100-p)". En el caso del promedio se tomaba en cuenta la varianza de la población, en este caso se toma en cuenta la proporción de la cualidad (por ejemplo sexo) que estamos estudiando en la población. La proporción se cuantifica en porcentajes, por ejemplo si analizáramos la población de alumnos de la facultad de medicina podríamos decir que se presenta 60 % de mujeres. La proporción es presentada en forma de prevalencia en muchos casos por ejemplo podríamos decir que la prevalencia de diabetes en la población de lima para este año es de 15 %.
Tamaño de muestra según la prevalencia:
Si prevalencia = 10%, n = 35
Si prevalencia = 20%, n = 62
Si prevalencia = 30%, n = 81
Si prevalencia = 40%, n = 93
Si prevalencia = 50%, n = 97
Si prevalencia = 60%, n = 93
Las curvas de la gráfica presentada arriba nos demuestran que a medida que la prevalencia aumenta el tamaño de la muestra crece hasta un tamaño máximo luego decrece de la misma forma en que se incrementa la prevalencia. El mayor tamaño de muestra se presenta cuando la prevalencia es del 50 %.
Los colores de las curvas asociados a porcentajes nos demuestran como el margen de error influye dramáticamente en el tamaño de la muestra. Con un margen de error de +- 2.5 % el tamaño de muestra es de aproximadamente 1500 unidades de estudio mientras que con un margen de error de +- 10% el tamaño de la muestra es tan solo de 100 unidades de estudio. Pequeños cambios en la formula producen cambios importantes en el tamaño de la muestra.
ESTUDIO ANALÍTICOConsisten en estudios donde se consideran mas de una variable. Podríamos estar en el caso bivariado o multivariado. En este tipo de estudio se busca comparar, asociaciones o correlaciones y en el mejor de los casos un relación de causa efecto entre la variable independiente y la variable dependiente. Se caracteriza porque se compara dos grupos muestrales para observar diferencias y luego estimar estas diferencias con el parámetro estudiado
PROMEDIO
En la formula presentada para el cálculo del tamaño de muestra para una variable cuantitativa (promedio en este caso), siendo el estudio analítico, se presentan algunas diferencias:
-poder estadístico: es una variable matemática que se incluye en los estudios analítico y que evidentemente tiene un efecto incremental en el tamaño de la muestra. Esto quiere decir que en algunos casos los estudios analíticos necesitan un tamaño de muestra superior al de los estudios descriptivos.
-diferencia de promedios: es una variable matemática de la formula que puede incrementar o disminuir el tamaño de la muestra considerablemente. Se trata de la diferencia entre los valores normales y patológicos de una enfermedad en muchos casos. Por ejemplo podríamos observar la diferencia entre los niveles de glucemia entre personas sin diabetes y otras con diabetes. Este el valor que debemos incluir en la fórmula.
A medida que las diferencias entre grupos muestrales comparados son mas pequeñas el tamaño de la muestra debe ser mayor.
1 veamos la siguiente imagen:
Es evidente que las diferencias son muy claras y fácilmente de identificar. Nos hemos tomado un tiempo mínimo en determinar si las dos imágenes son diferentes o no. De la misma manera cuando dos grupos son muy diferentes las muestras necesarias también son pequeñas.
2 ahora veamos otra imagen:
Es evidente que las diferencias no son muy claras y fácilmente de identificar. Nos hemos tomado un tiempo muy amplio en determinar si las dos imágenes son diferentes o no. De la misma manera cuando dos grupos no son muy diferentes las muestras necesarias también deben ser grandes.
Muchas veces las diferencias son tan pequeñas que los tamaños de muestras se hacen muy grandes hasta ser imposibles. Cuando las diferencias son tan pequeñas es posible que el estudio no obtenga resultados significativos para su utilidad practica. De esta forma debemos evaluar si la investigación que deseamos hacer merece la pena ser realizada o no.
PROPORCIÓN
Parámetros necesarios:
Zβ = valor Z del poder estadístico.
Zα = Valor Z del nivel de confianza.
p(100-p) = variabilidad de “p1-p2: es un factor de debemos obtener de la bibliografía.
(p1-p2): es un factor que debemos determinar restando las prevalencias en cada uno de los dos grupos comparados.
FACTIBILIDAD EN EL TAMAÑO DE LA MUESTRA
Esta tabla nos muestra, que consideraciones debemos tomar durante la toma de muestra para obtener el objetivo deseado. Partimos del tamaño de muestra calculado y luego vamos incrementando el numero de esta a medida que consideramos otros factores que pueden influir directamente en la factibilidad de que una unidad de análisis sea o no parte de la muestra. Son muchos factores los que pueden terminar sacando de la muestra a la unidad muestral por ello debemos considerar un tamaño de muestra mayor en el momento de obtener los datos. Durante el procesamiento estadístico de los datos serán depurados aquellas unidades de estudio que no cumplan, por uno u otro motivo, con los requerimientos del estudio.
TEOREMA DEL LIMITE CENTRAL
Una distribución de probabilidades es una
función ƒ(x) que asigna, a cada suceso (valor de la variable, evento u observación), la
probabilidad de que dicho suceso
ocurra. Para poder realizar el cálculo estadístico necesitamos una muestra con distribución normal. Muchas veces ocurre que la población estudiada no tiene este tipo de distribución de probabilidades y por lo tanto no podríamos realizar los cálculos adecuadamente ya que las fórmulas utilizadas están hechas para el modelo de distribución normal. Una población con distribución normal se caracteriza porque los valores mas frecuentes se concentran en el medio de la campana de distribución y los valores extremos en las colas de la campana de distribución. Esta es la forma de distribución de probabilidades para el que están diseñadas las pruebas estadísticas. Cuando estudiamos una población que no posee una distribución normal, por ejemplo una distribución uniforme, existe la posibilidad de poderla estudiar considerando el teorema del limite central:
La distribución del promedio de “n”
muestras de tamaño ≥30 tendrán una distribución normal, sin importar
la distribución de la población de origen.
En la imagen de arriba observamos en la primera fila las gráficas de algunas distribuciones que no se distribuyen en forma de campana de Gaus. Pero si tomamos muestras a partir de la población y distribuimos sus respectivos promedios la forma de distribución va cambiando. A medida que los tamaños de muestras se acercan a treinta obtenemos distribuciones muestrales cada vez más parecidas a la distribución normal.
De esta manera una muestra sin distribución normal de probabilidad puede ser estudiada adecuadamente. Hasta este momento habíamos estudiado la distribución de probabilidad de las observaciones o eventos hechas sobre una variable. En el T.L.C lo que distribuiremos son las diferentes posibles muestras tomadas de una población, por lo tanto se trata de una distribución muestral del estadístico que podría ser un promedio una proporción o cualquier otro estadístico. Sabemos que existe un numero determinado de posibles muestras que se pueden extraer de una población de cierto tamaño, generalmente si la población tiene un numero considerable de individuos la cantidad de posibles muestras es abrumadora, por ejemplo si disponemos de una población de 10 individuos y elegimos a 2 de ellos la cantidad posible de muestras en las que no se repitan los arreglos es de 45, ahora pensemos en una población de 20 individuos y seleccionamos muestras de 4 individuos sin que se repitan las combinaciones entonces tendríamos 4845 posibles muestras. El numero de muestras depende del tamaño de cada muestra y del tamaño de la población. Si pudiéramos obtener todas las muestras posibles de una población entonces podríamos calcular el promedio de cada una de las muestras y distribuir este promedio. El resultado es realmente sorprendente, la distribución del promedio de todas las muestras posibles de una población sin distribución normal genera una distribución normal de probabilidad con la ventaja de poder trabajar sobre ella adecuadamente. La sorpresa es aun más grande cuando nos damos cuenta de que el estadístico estudiado, por ejemplo el promedio de la distribución de las muestras coincide exactamente con el promedio del parámetro poblacional. Esto solamente ocurre cuando distribuimos los promedios de todas las muestras posibles de una población.
Está claro que otra vez tenemos una limitación: no es posible distribuir todas las muestras posibles de una población. Ni siquiera trabajamos con algunas muestras. Normalmente para una investigación debemos trabajar solamente con una muestra lo cual ha sido el tema de todo este capítulo.
Considerando la idea de que podemos obtener el promedio poblacional a partir del promedio de la distribución de todas las muestras podemos permitirnos una aproximación interesante a partir de un tamaño de muestra ideal.
Resulta más interesante aun que a partir de la distribución de las muestras obtenidas de una población se puede calcular la desviación estándar propia de esta distribución a la cual denominamos error estándar.
Como no es posible obtener todas las muestras posibles de una población y por lo tanto obtener su desviación estándar, a la cual a partir de ahora llamaremos error estandar, debemos calcular este factor importante de otra forma:
Resulta más interesante aun que a partir de la distribución de las muestras obtenidas de una población se puede calcular la desviación estándar propia de esta distribución a la cual denominamos error estándar.
El error estándar no es mas que la variabilidad que existe en la distribución de probabilidad de todas las muestras de una población.
Como no es posible obtener todas las muestras posibles de una población y por lo tanto obtener su desviación estándar, a la cual a partir de ahora llamaremos error estandar, debemos calcular este factor importante de otra forma:
Es el cociente entre la desviación estándar de la muestra y la raíz cuadrada del tamaño de la muestra.
Error Estándar = s/√n
Es evidente que el error estándar depende fundamentalmente del tamaño de la muestra que tengamos. Un error estándar menor se logrará cuando la muestra sea de tamaño considerable. Si el tamaño de la muestra es menor entonces el error estándar es grande de manera que la variabilidad en la distribución de las muestras sería muy grande y la probabilidad de que nos acerquemos con nuestros resultados al promedio poblacional es menor. Por ejemplo imaginemos que estamos en busca de una persona y nos encontramos frente a dos escenarios posibles: en el primer caso intentamos buscar a una persona en un lugar muy grande, del tamaño de dos estadios juntos. Adicionemos a esta circunstancia que estamos en presencia de una gran multitud de personas. Es evidente que encontrar a la persona que buscamos sería muy difícil ya que es muy probable que estemos a una gran distancia de esta persona. En el segundo caso estamos en un escenario diferente es un local pequeño algo así como una discoteca, es cierto que también hay bastante gente pero la distancia a la que nos encontramos de la persona es sin lugar a dudas mucho menor que en el primer caso. De esta forma la probabilidad de estar cerca de la persona a la que deseamos encontrar es mucho mayor. De la misma forma la distribución muestral de un estadístico pueden tener mayor o menor dispersión tal y como en nuestros ejemplos de esta manera la probabilidad de estar cerca del parámetro depende de la variabilidad y la dispersión. Recordemos que la probabilidad de los eventos de una distribución normal dependen de la media y de la desviación estándar (que en este caso se denomina error estándar). Si la desviación estándar varia, entonces la probabilidad de un determinado evento de la distribución también.
A través del error estándar podemos cuantificar la precisión de nuestro estudio, es decir sabemos a ciencia cierta cual es la incertidumbre de nuestros resultados. Dicho de otra forma el error estándar es la medida de la probabilidad de acercarnos al parámetro verdadero.
Es bueno aclarar que debemos llegar a un punto de equilibrio entre el tamaño de muestra y el error estándar. Mientras mas grande es la muestra más costosa es la investigación y podremos tomar un error estándar mínimo. Un tamaño de nuestra muy pequeño incrementa el error estándar considerablemente y la probabilidad de acercarnos al parámetro de la población bajo estudio es lejana. No es bueno exagerar en ninguno de los dos sentidos.
LA INFERENCIA ESTADÍSTICA POR ESTIMACIÓN DE PARÁMETROS
Los dos procedimientos para realizar la inferencia estadística son:
- Estimación de parámetros
- Pruebas de hipótesis estadísticas
Estimar en general significa asignar un valor basándonos en juicios o en la experiencia de un experto en el tema. En estadística estimar significa asignar valores a los parámetros a partir de los datos de la muestra.
Existen dos formas de estimar parámetros:
- Estimado puntual: se da cuando asignamos un solo valor a un parámetro. Ejemplo de estimado puntual es el valor del estadístico que obtenemos a partir de la muestra aleatoria sobre la cual estamos trabajando, ya sea un promedio o una proporción.
- Intervalo de confianza: se hacen suposiciones o conjeturas que realiza un conocedor de los parámetros. Estas hipótesis o conjeturas deben ser verificadas. Estimar por medio de un intervalo de confianza significa dar un rango de valores posibles dentro del cual se encontraría el parámetro buscado. Es cierto que no tenemos la completa certeza de que el intervalo de confianza capture al parámetro, pero es suficiente como para garantizar el éxito del estudio.
La imagen de arriba nos ilustra amablemente la diferencia entre un estimado puntual y de intervalo. El estimado puntual( promedio, proporción muestral) trata de "capturar" al parámetro poblacional como un pescador lo haría con una lanza. Es evidente que la probabilidad de que "pesque" al parámetro poblacional es bastante reducida. Si en vez de tratar de pescar el parámetro con una lanza lo hacemos con una red las probabilidades de dar con el parámetro se incrementa considerablemente. El intervalo de confianza hace lo mismo que la red de pescar, al considerar un rango de valores posibles del parámetro dentro del mismo. Por supuesto a pesar de que las probabilidades de "pescar" al parámetro han aumentado mucho no tenemos la seguridad o confianza de haberlo hecho al 100 %. Es común tener un nivel de confianza bastante alto tanto como el 95% de seguridad de haber dado con el parámetro dentro del intervalo de confianza.
Estos cálculos se hacen con un cierto nivel de incertidumbre por lo cual debemos hacer uso de la probabilidad como herramienta de calculo matemático. Decimos que :
La
probabilidad permite calibrar el poder o alcance de las conclusiones, en
condiciones de incertidumbre.
Tratándose de la estimación debemos asignar una probabilidad de confianza o nivel de confianza. Por ejemplo si decimos que la prevalencia de una enfermedad es del 20-30 % entonces debemos dejar claro cuáles son las condiciones de incertidumbre o en su defecto con cuanta certeza es que se enuncia esta probabilidad.
La estimación es un proceso mediante el cual a partir de los valores de una variable obtenida de la muestra aleatoria se puede estimar dando un solo valor para la estimación puntual o dando un conjunto de valores a través de la estimación por intervalos con la intención de aproximarnos al valor del parámetro. Esto no quiere decir que el parámetro sea necesariamente el valor estimado, para el caso de la estimación puntual y tampoco todo el conjunto de posibles valores para el caso de la estimación por intervalos, sino que es una estimación sustentada por la probabilidad de confianza. Por lo tanto decimos que ya sea una estimación puntual o un intervalo de valores se trata solamente de posibles valores, ello indica que es posible que no lo sean. Para medir la posibilidad de que el valor(puntual) o los valores propuestos(intervalo) son los reales se hace uso del nivel confianza.
Se acostumbra a designar al parámetro: θ
La estimación es el uso estricto de la información muestral basándonos en la probabilidad, para poder extraer información sobre el parámetro de la población.
La estimación es el uso estricto de la información muestral basándonos en la probabilidad, para poder extraer información sobre el parámetro de la población.
¿Qué herramienta vamos a utilizar para estimar el
parámetro? Utilizaremos la contraparte del parámetro: el estadístico.
El estadístico que sirve para estimar el parámetro se
denomina ESTIMADOR:
El estimador es una función matemática que solamente depende de
valores muestrales o de información muestral a partir de la muestra aleatoria.
Cuando ya hemos hecho el cálculo respectivo empleando
el estimador el valor resultante se
denomina: ESTIMACIÓN. Por ejemplo si se calcula la prevalencia de diabetes para
este mes es del 30% entonces la estimación es 0.30.
En el contexto de la estadística inferencial decimos
que los estimadores estadísticos tales como la varianza, media o proporción
muestral van a estimar a la varianza, media y proporción poblacional
respectivamente. Con esto se quiere decir que a partir de los valores
estadísticos se puede generalizar hasta llegar a los valores de toda la
población con cierto nivel de probabilidad.
el
proceso mediante el cual se efectúan generalizaciones para la población bajo
estudio a partir de los resultados de una muestra aleatoria extraída de esta,
se le llama inferencia estadística (ie)
Como veremos al determinar cualquier estadístico de una
muestra aleatoria estos también tendrán la propiedad de ser
aleatorios.
El investigador tomará durante la selección de la muestra una muestra
aleatoria de las varias muestras aleatoria posibles, vemos así que existe
variabilidad en este proceso al igual que incertidumbre por lo cual la mejor
forma de obtener y sustentar la información es a través de la probabilidad. Por otro lado los
estadísticos que obtenemos de estas muestras aleatorias están sujetos a las mismas condiciones de variabilidad e incertidumbre. El error de muestreo es un concepto clave en este punto. Significa que debido a la incertidumbre es decir el azar y a la variabilidad natural de los fenómenos observables, la muestra tomada puede generar estadísticos más o menos alejados del verdadero parámetro población. Para explicar esto mejor hagamos un experimento mental: Pensemos en uno de los ejemplos presentados más arriba. Dijimos que existían 4845 posibles muestras de 4 individuos de un total 20 que formaban nuestra población. Si estudiáramos algún parámetro de la población, por ejemplo el promedio de alguna característica en concreto y esta es "X" un valor desconocido para nosotros y al que solamente podemos conocer por medio de un estadístico muestral. Entonces solamente podríamos estudiar una de las 4845 muestras posibles elegida de forma aleatoria. Es cierto que el promedio de nuestra muestra elegida al azar podría acercarse bastante al promedio de la población y ser una buena estimación pero también es posible que la muestra elegida no se parezca mucho a la población estudiada y por lo tanto haríamos una mala estimación del parámetro. expliquemos un poco mejor esto. Los individuos que constituyen una población no presentan la característica estudiada en la misma medida o en la misma magnitud debido a que la variabilidad es una condición inherente de las variables físicas, biológicas o sociales, por lo tanto existe un rango de variabilidad caracterizado por una distribución que en muchos casos sigue de forma natural el modelo de la distribución normal. Lo más importante está en entender que cuando se forman las muestras, de manera que cada muestra es una combinación diferente de las 4845 muestras posibles existen algunos arreglos (muestra) que reúnen a individuos que tienen una magnitud de la variable estudiada muy cercana al promedio de la población, además este tipo de arreglos son la mayoría(cerca del 95% de ellas, para nuestro ejemplo serían 4602),mientras que otros arreglos estarían formados por los individuos que tienen una magnitud de la variable estudiada alejada del promedio de la población, además estos son pocos, algo menores al 5 % por lo general. Debido a que la selección de la muestra es aleatoria no sabemos con exactitud cual de las muestras será con la que tengamos que realizar las estimaciones. Es cierto que existe una mayor probabilidad de seleccionar al azar una muestra cuyo estadístico sea bastante similar al parámetro de la población pero no estamos completamente seguro de ello, además esta situación en la que existe una gran probabilidad de seleccionar una muestra al azar sabiendo de antemano que existen mayores probabilidades de elegir una que se parezca a la población solamente se da en el caso de que hagamos la selección de la muestra en condiciones de completa aleatoriedad. Si somos pesimistas podríamos pensar en que nuestra selección fue lamentablemente una muestra que se aleja de los valores promedios. Aunque la estimación del parámetro con esta muestra sea bastante malo no debemos olvidar que esa muestra pertenece a la población con la cual estamos trabajando, más adelante veremos que esta situación es la base de las pruebas de hipótesis.
ESTIMACIÓN POR INTERVALOS
Estimar por intervalos significa obtener un intervalo numérico, estos
están limitados por un límite inferior y un límite superior. Para determinar y validar este intervalo tenemos que asociarle o asignarle una probabilidad. A esta probabilidad se
le denomina DE CONFIANZA o también NIVEL DE CONFIANZA. Nos permite saber la
certidumbre o la confianza de que el parámetro probablemente este contenido
entre el límite inferior y el límite superior. Es importante remarcar que no se
puede afirmar categoricamente que el parámetro este contenido entre estos límites sino que
probablemente se encuentre ahí lo cual indica un cierto nivel de incertidumbre
aunque sea mínimo.
La probabilidad de confianza es seleccionada
responsablemente por el investigador
El intervalo de confianza se determina mediante la siguiente formula:
El intervalo de confianza es un conjunto de valores desde un mínimo a un máximo que resulta de la resta y la suma de un valor determinado al estadístico en cuestión. El valor que debemos sumar y restar al estadístico, llamado margen de error, resulta de la multiplicación del nivel de confianza elegido y el error estándar, que estudiamos más arriba.
Error Estándar = s/√n
El margen de error entonces es un porcentaje, ya que el error estándar se presenta en forma de porcentaje. Este margen de error es el que amplía o disminuye el intervalo de confianza. Depende del nivel de confianza, a mayor nivel de confianza el margen de error será mayor y por lo tanto el intervalo de confianza también crecerá. El efecto final es el crecimiento del intervalo de confianza. El margen de error también puede aumentar si el error estándar aumenta. Sabemos que el error estándar depende de la desviación estándar de la muestra y de el tamaño de la muestra. La desviación estándar es propia de la muestra tomada y no depende el investigador. Una muestra muy pequeña hará que el error estándar sea grande y este a su vez influenciará en el valor del margen de error y finalmente hará que el intervalo de confianza se amplié. El error estándar cuantifica la dispersión de la distribución de las medias muestrales y por lo tanto constituye un valor que influye directamente sobre el intervalo de confianza. Un error estándar grande proviene de una distribución muestral en donde las medias muestrales se alejan considerablemente del promedio poblacional, todo lo contrario ocurre con un error estándar pequeño. Recordemos que la dispersión de las medias muestrales depende del tamaño de las muestras. Es lógico que el intervalo de confianza sea un reflejo de la distribución muestral, generado a través del error estándar. Diremos entonces que el intervalo de confianza depende fundamentalmente del tamaño de la muestra. A mayor tamaño de muestra el intervalo de confianza será menor, mientras que a menor tamaño de muestra el intervalo de confianza correspondiente será mayor.
Más abajo analizaremos en detalle el papel relevante que juega el nivel de confianza en el tamaño del intervalo.
Para dar un alcance muy sencillo de lo que estamos explicando supondremos un estadístico y su correspondiente margen de error de manera que podamos darnos cuenta de que manera funcionan los intervalos de confianza:
Supongamos que tras nuestro estudio determinamos que la prevalencia de diabetes en lima será de 18 % +-3% con una nivel de confianza del 95%. Esto quiere decir que el parámetro poblacional, es decir el verdadero valor que estamos tratando de estimar puede encontrarse entre 15% a 21 % de prevalencia para esta enfermedad. Entonces el intervalo de confianza es: 15% a 21 % con el 95% de confianza.
Ahora veamos algunos ejemplo un poco más elaborados:
En la imagen mostrada arriba se observa que cada barra horizontal (20 en total) representa el intervalo de confianza de 20 muestras. Aunque no se note claramente el centro de cada barra horizontal representa el estadístico de la muestra(estimación puntual). La línea vertical representa el parámetro de la población. 19 de cada 20 intervalos de confianza "capturan" al parámetro. Se observa que uno de los parámetros (barra horizontal roja) no captura al parámetro y representa el 5 % de todos los intervalos de confianza posibles. Esta situación demuestra que una gran proporción (95%) de las muestras y de sus respectivos intervalos de confianza logran contener al parámetro. Si bien el estadístico no coincide con el parámetro, en un gran porcentaje si lo hacen los intervalo de confianza. Es evidente que si utilizamos un nivel de confianza alto los intervalos de confianza serán capaces de contener al parámetro buscado. Aunque no sepamos exactamente cual es el parámetro tendremos una gran seguridad de que esta contenido en el parámetro generado a partir de la muestra aleatoria.
Nuevamente recordemos que a medida que el tamaño de las muestras aleatorias posibles de una población sean mayores la posibilidad de que los estadísticos que obtengamos de estas muestras se acerque considerablemente al parámetro es mayor. Si el estadístico de la muestra se aproxima mucho al parámetro el intervalo de confianza que obtengamos de esta muestra, casi con seguridad, contendrá al parámetro poblacional. A medida que el tamaño de la muestra es mayor el intervalo de confianza es más estrecho manteniéndose el nivel de confianza alto. Esto se debe a que el intervalo de confianza tiene una mayor probabilidad de contener al parámetro. Observamos en la imagen de arriba que no todas las barras tienen el mismo tamaño a pesar de que todas las barras que representan al intervalo de confianza tienen el mismo nivel de confianza y el mismo tamaño de muestra esto se debe a que la desviación estándar en cada muestra es ligeramente diferente.
Un detalle importante de recordar es que siempre debemos enunciar esta situación del siguiente modo:
"Con un nivel de confianza x (normalmente 1.96) el intervalo de confianza captura o contiene al parámetro poblacional."
No debemos enunciarlo de otra forma ya que estaría cometiendo un error. A veces se acostumbra a decir que con un nivel de confianza determinado el parámetro esta contenido en un determinado intervalo de confianza lo cual no es correcto.
respuesta: FVFF
CERTEZA Y PRECISIÓN
La certeza de capturar al parámetro se incrementa a medida que el intervalo de confianza aumenta en su amplitud. Un intervalo de confianza grande nos asegura en mayor medida que el parámetro buscado se encuentre dentro del intervalo. La pregunta que nos debemos hacer es hasta qué punto deberíamos aumentar la certeza. Esta cualidad de la estimación del parámetro debe estar justificada por el grado de utilidad de la estimación. La utilidad del estadístico, es decir el intervalo, se caracteriza por su precisión. Si el intervalo de confianza es pequeño y contiene al parámetro entonces la precisión es alta, por el contrario un parámetro demasiado amplio le resta mucha precisión al intervalo de confianza. Cuanta mayor precisión tenga el parámetro mayor utilidad tendrá. La Utilidad del parámetro se demuestra cuando podemos tomar decisiones a partir del intervalo de confianza y estar seguros de que nuestros acciones no serán defraudadas por una situación diferente a la planteada por el intervalo. La mejor forma de tener un intervalo de confianza certero y preciso es aumentando el tamaño de la muestra. Recordemos el caso que presentamos más arriba sobre el pronostico de la temperatura.
La imagen de arriba nos da amablemente una idea de la poca utilidad de un intervalo de confianza muy amplio. El intervalo de confianza "c" posee una amplitud muy grande de forma que aunque se logra una certeza importante con este intervalo se tiene muy poca precisión porque cualquier decisión que tomemos en base a este intervalo sería muy ambigua y poco útil con una gran posibilidad de equivocarnos. Tomemos en cuenta que ciencias de la salud es más que recomendable tener un grado de precisión muy grande debido a que normalmente las decisiones que se tomen en base a los estadísticos propuestos pueden comprometer la vida de los pacientes.
Ejemplo:
FORMULACIÓN:
El intervalo de confianza se determina mediante la siguiente formula:
El intervalo de confianza es un conjunto de valores desde un mínimo a un máximo que resulta de la resta y la suma de un valor determinado al estadístico en cuestión. El valor que debemos sumar y restar al estadístico, llamado margen de error, resulta de la multiplicación del nivel de confianza elegido y el error estándar, que estudiamos más arriba.
Error Estándar = s/√n
El margen de error entonces es un porcentaje, ya que el error estándar se presenta en forma de porcentaje. Este margen de error es el que amplía o disminuye el intervalo de confianza. Depende del nivel de confianza, a mayor nivel de confianza el margen de error será mayor y por lo tanto el intervalo de confianza también crecerá. El efecto final es el crecimiento del intervalo de confianza. El margen de error también puede aumentar si el error estándar aumenta. Sabemos que el error estándar depende de la desviación estándar de la muestra y de el tamaño de la muestra. La desviación estándar es propia de la muestra tomada y no depende el investigador. Una muestra muy pequeña hará que el error estándar sea grande y este a su vez influenciará en el valor del margen de error y finalmente hará que el intervalo de confianza se amplié. El error estándar cuantifica la dispersión de la distribución de las medias muestrales y por lo tanto constituye un valor que influye directamente sobre el intervalo de confianza. Un error estándar grande proviene de una distribución muestral en donde las medias muestrales se alejan considerablemente del promedio poblacional, todo lo contrario ocurre con un error estándar pequeño. Recordemos que la dispersión de las medias muestrales depende del tamaño de las muestras. Es lógico que el intervalo de confianza sea un reflejo de la distribución muestral, generado a través del error estándar. Diremos entonces que el intervalo de confianza depende fundamentalmente del tamaño de la muestra. A mayor tamaño de muestra el intervalo de confianza será menor, mientras que a menor tamaño de muestra el intervalo de confianza correspondiente será mayor.
Margen de error=Nivel de confianza x E.E
Más abajo analizaremos en detalle el papel relevante que juega el nivel de confianza en el tamaño del intervalo.
Supongamos que tras nuestro estudio determinamos que la prevalencia de diabetes en lima será de 18 % +-3% con una nivel de confianza del 95%. Esto quiere decir que el parámetro poblacional, es decir el verdadero valor que estamos tratando de estimar puede encontrarse entre 15% a 21 % de prevalencia para esta enfermedad. Entonces el intervalo de confianza es: 15% a 21 % con el 95% de confianza.
Ahora veamos algunos ejemplo un poco más elaborados:
ejemplo:
Sobre asimetría en el
comportamiento;
Un estudio en 124 parejas encontró que 64.5% de estas inclinaba la cabeza hacia la derecha al momento de besarse. El error estándar de este estimado fue 4% aprox. ¿Qué enunciado es falso?
Un estudio en 124 parejas encontró que 64.5% de estas inclinaba la cabeza hacia la derecha al momento de besarse. El error estándar de este estimado fue 4% aprox. ¿Qué enunciado es falso?
A Un mayor tamaño de
muestra mayor reduciría el error estándar.
B El margen de error para
un IC95% del porcentaje de parejas que
inclina su cabeza hacia la derecha es 8%.
C El IC95% del porcentaje
de parejas que inclina su cabeza hacia
la derecha es 64.5% ± 4%.
D El IC99.7% del
porcentaje de parejas que inclina su
cabeza hacia la derecha es 64.5% ± 12%.
respuesta: c
NIVEL DE CONFIANZA
Si tomamos varias muestras de tamaño “n” y construimos sus intervalos de confianza
El nivel de confianza
es la proporción de ICs que contienen el valor poblacional.
Nuevamente recordemos que a medida que el tamaño de las muestras aleatorias posibles de una población sean mayores la posibilidad de que los estadísticos que obtengamos de estas muestras se acerque considerablemente al parámetro es mayor. Si el estadístico de la muestra se aproxima mucho al parámetro el intervalo de confianza que obtengamos de esta muestra, casi con seguridad, contendrá al parámetro poblacional. A medida que el tamaño de la muestra es mayor el intervalo de confianza es más estrecho manteniéndose el nivel de confianza alto. Esto se debe a que el intervalo de confianza tiene una mayor probabilidad de contener al parámetro. Observamos en la imagen de arriba que no todas las barras tienen el mismo tamaño a pesar de que todas las barras que representan al intervalo de confianza tienen el mismo nivel de confianza y el mismo tamaño de muestra esto se debe a que la desviación estándar en cada muestra es ligeramente diferente.
Un detalle importante de recordar es que siempre debemos enunciar esta situación del siguiente modo:
"Con un nivel de confianza x (normalmente 1.96) el intervalo de confianza captura o contiene al parámetro poblacional."
No debemos enunciarlo de otra forma ya que estaría cometiendo un error. A veces se acostumbra a decir que con un nivel de confianza determinado el parámetro esta contenido en un determinado intervalo de confianza lo cual no es correcto.
ejemplo:
Basados en una encuesta a
1154 peruanos, el IC95% del promedio de
horas dedicadas al “ocio” después de
trabajar fue de 3.53 a 3.83 horas. Diga V o F.
A El 95% de peruanos
dedica de 3.53 a 3.83 horas al “ocio”
después de trabajar.
B El 95% de muestras
aleatorias de 1154 peruanos tendrán IC
que contengan el verdadero promedio de horas que los peruanos dedican al ocio después de
trabajar.
C El 95% de las veces, el
verdadero promedio de horas que los
peruanos dedican al ocio después de trabajar está entre 3.53 y 3.83 horas.
D Tenemos 95% de confianza
que los peruanos de esta muestra
dedicaron entre 3.53 y 3.83 horas al ocio
después de trabajar.
CERTEZA Y PRECISIÓN
La certeza de capturar al parámetro se incrementa a medida que el intervalo de confianza aumenta en su amplitud. Un intervalo de confianza grande nos asegura en mayor medida que el parámetro buscado se encuentre dentro del intervalo. La pregunta que nos debemos hacer es hasta qué punto deberíamos aumentar la certeza. Esta cualidad de la estimación del parámetro debe estar justificada por el grado de utilidad de la estimación. La utilidad del estadístico, es decir el intervalo, se caracteriza por su precisión. Si el intervalo de confianza es pequeño y contiene al parámetro entonces la precisión es alta, por el contrario un parámetro demasiado amplio le resta mucha precisión al intervalo de confianza. Cuanta mayor precisión tenga el parámetro mayor utilidad tendrá. La Utilidad del parámetro se demuestra cuando podemos tomar decisiones a partir del intervalo de confianza y estar seguros de que nuestros acciones no serán defraudadas por una situación diferente a la planteada por el intervalo. La mejor forma de tener un intervalo de confianza certero y preciso es aumentando el tamaño de la muestra. Recordemos el caso que presentamos más arriba sobre el pronostico de la temperatura.
La imagen de arriba nos da amablemente una idea de la poca utilidad de un intervalo de confianza muy amplio. El intervalo de confianza "c" posee una amplitud muy grande de forma que aunque se logra una certeza importante con este intervalo se tiene muy poca precisión porque cualquier decisión que tomemos en base a este intervalo sería muy ambigua y poco útil con una gran posibilidad de equivocarnos. Tomemos en cuenta que ciencias de la salud es más que recomendable tener un grado de precisión muy grande debido a que normalmente las decisiones que se tomen en base a los estadísticos propuestos pueden comprometer la vida de los pacientes.
Ejemplo:
Un grupo de investigadores
desea evaluar el posible efecto de tomar
medicamentos para la epilepsia durante
la gestación en el desarrollo cognitivo de los
niños. Estudios previos sugieren que la desviación estándar (s) del IQ de niños de 3 años es 18
puntos.
¿Cuántos niños deben
incluirse en el estudio para tener un IC95% con un margen de error ≤ 4 puntos?
FORMULACIÓN:
1-α nos indica el grado de certeza de que
el parámetro se encuentra entre limite inferior(LI) y el límite superior (LS).
Sabemos que la probabilidad toma valores entre 0 (mínimo)y 1(máximo) por lo que 1- α es conveniente que se acerque a uno. Para ello α debe ser un
valor positivo, pero muy pequeño de manera que exista una alta probabilidad de
que el parámetro se encuentre entre los limites del parámetro.
El valor de α que es normalmente asignado por los investigadores es de
0,05 o 5 % lo cual quiere decir que el grado de certeza de que el parámetro se
encuentre dentro del intervalo debe ser en teoría de 95 % o que 19 IC de un total de 20 IC contienen con seguridad el parámetro. El IC se encuentra asociado a cada una de las muestras de entre una determinada cantidad de muestras aleatorias posibles. Cuando escogemos una muestra a partir de una población estamos seleccionando de forma aleatoria una muestra de entre muchas otras. Este proceso de selección es lo que genera cierta incertidumbre (error de muestreo) que se expresa matemáticamente mediante el nivel de confianza. Por lo tanto al estar asociado un IC a cada muestra posible, los IC variarán en la misma forma que varían las muestras. Tanto las posibles muestras como los IC poseen la variabilidad e incertidumbre propias de procesos probabilísticos.
El error de muestreo se corrige mediante el uso de intervalos de confianza, a mayor error de muestreo mayor debe ser el intervalo de confianza para evitar el sesgo de muestreo.
El nivel de confianza del intervalo de confianza normalmente es el mismo que el usado para calcular el tamaño de la muestra. Muestra e intervalo de confianza tienen características similares. Se podría decir que el intervalo de confianza depende de la muestra de la que proviene. Por lo tanto cada muestra tiene su propio intervalo de confianza asociado.
EL NIVEL DE CONFIANZA SIGUE UN PATRÓN DE DISTRIBUCIÓN NORMAL
El nivel de confianza se basa en la distribución normal de probabilidad. Quiere decir que los valores de probabilidad son tomados en base a la cantidad de desviaciones estándar que determina cada investigador. Normalmente se toman dos desviaciones (1.96 para ser precisos). El área bajo la curva de la distribución es la probabilidad acumulada que nosotros deseamos para asegurarnos de que en la mayor medida el promedio muestral se acerque al parámetro de la población. Es decir el intervalo de confianza se fundamenta en una distribución normal de probabilidad en la que consideramos comúnmente dos desviaciones estándar para asegurarnos de que dentro del intervalo se encuentre el parámetro de la población.
El intervalo de confianza constituye en realidad un conjunto de valores de la variable aleatoria, por ejemplo si se trata del promedio de hemoglobina en sangre de una muestra aleatoria(16 mg/dl) el intervalo podría ser +/- 3 mg/dl (de 13 a 19 mg/dl). Todos los valores de hemoglobina en sangre comprendidos entre estos valores constituyen el el 95 % central de valores, si el nivel de confianza fue el de 95%. Como es evidente, al tratarse de una variable continua los valores posibles son bastante numerosos. Pero lo más importante es que todos estos valores están distribuidos siguiendo el modelo de una distribución normal. De esta forma podemos calcular la probabilidad de cada valor de la variable a través de los percentiles de desviación estándar. El intervalo de confianza puede ser analizado y establecido a través de una distribución de probabilidad normal conveniente para estimar adecuadamente el parámetro que buscamos. Si establecemos un nivel de confianza alto(95%) esto correspondería a 1.96 desviaciones estándar lo cual significa que el intervalo considera una gran cantidad de posibles valores del estadístico en cuestión. Para nuestro ejemplo sería de 13 a 19 mg/dl). supongamos que disminuimos el nivel de confianza al 80 % esto quiere decir que se considerará una desviación estándar menor a 1.96 de forma que los valores que se consideren en el intervalo de confianza son menores por ejemplo de 15 a 17 (+/-2mg/dl). de esta forma a medida que disminuimos el nivel de confianza la amplitud de del intervalo de confianza disminuye. Siempre es recomendable tomar un alto nivel de confianza, pero teniendo en cuenta que el intervalo no se haga demasiado grande como para ser de poca utilidad en el estudio.
En la distribución normal de probabilidad del intervalo de confianza las “colas” representan la probabilidad de los eventos con menos y mayor valor (por ejemplo glucemia o colesterol sérico) mientras que en el centro se encuentra los de mayor probabilidad el cual corresponde a valores intermedios de la variable.
No es lo mismo obtener un intervalo con el 95%(19 muestras de 20) de probabilidad de confianza que obtener uno del 90%(18 muestras de 20) de probabilidad de confianza. En el primer caso, en 19 muestras de 20, con seguridad, se encuentra el parámetro que deseamos calcular. De forma complementaria en 1 de 20 muestras no contiene el parámetro deseado, es precisamente este el error que corresponde al 5%. No podemos saber realmente donde esta el parámetro dentro del intervalo, sin embargo, podemos decir con una confianza del 95 % que el intervalo con los limites superior e inferior respectivos contienen el valor real.
EL NIVEL DE CONFIANZA SIGUE UN PATRÓN DE DISTRIBUCIÓN NORMAL
El nivel de confianza se basa en la distribución normal de probabilidad. Quiere decir que los valores de probabilidad son tomados en base a la cantidad de desviaciones estándar que determina cada investigador. Normalmente se toman dos desviaciones (1.96 para ser precisos). El área bajo la curva de la distribución es la probabilidad acumulada que nosotros deseamos para asegurarnos de que en la mayor medida el promedio muestral se acerque al parámetro de la población. Es decir el intervalo de confianza se fundamenta en una distribución normal de probabilidad en la que consideramos comúnmente dos desviaciones estándar para asegurarnos de que dentro del intervalo se encuentre el parámetro de la población.
El intervalo de confianza constituye en realidad un conjunto de valores de la variable aleatoria, por ejemplo si se trata del promedio de hemoglobina en sangre de una muestra aleatoria(16 mg/dl) el intervalo podría ser +/- 3 mg/dl (de 13 a 19 mg/dl). Todos los valores de hemoglobina en sangre comprendidos entre estos valores constituyen el el 95 % central de valores, si el nivel de confianza fue el de 95%. Como es evidente, al tratarse de una variable continua los valores posibles son bastante numerosos. Pero lo más importante es que todos estos valores están distribuidos siguiendo el modelo de una distribución normal. De esta forma podemos calcular la probabilidad de cada valor de la variable a través de los percentiles de desviación estándar. El intervalo de confianza puede ser analizado y establecido a través de una distribución de probabilidad normal conveniente para estimar adecuadamente el parámetro que buscamos. Si establecemos un nivel de confianza alto(95%) esto correspondería a 1.96 desviaciones estándar lo cual significa que el intervalo considera una gran cantidad de posibles valores del estadístico en cuestión. Para nuestro ejemplo sería de 13 a 19 mg/dl). supongamos que disminuimos el nivel de confianza al 80 % esto quiere decir que se considerará una desviación estándar menor a 1.96 de forma que los valores que se consideren en el intervalo de confianza son menores por ejemplo de 15 a 17 (+/-2mg/dl). de esta forma a medida que disminuimos el nivel de confianza la amplitud de del intervalo de confianza disminuye. Siempre es recomendable tomar un alto nivel de confianza, pero teniendo en cuenta que el intervalo no se haga demasiado grande como para ser de poca utilidad en el estudio.
En la distribución normal de probabilidad del intervalo de confianza las “colas” representan la probabilidad de los eventos con menos y mayor valor (por ejemplo glucemia o colesterol sérico) mientras que en el centro se encuentra los de mayor probabilidad el cual corresponde a valores intermedios de la variable.
No es lo mismo obtener un intervalo con el 95%(19 muestras de 20) de probabilidad de confianza que obtener uno del 90%(18 muestras de 20) de probabilidad de confianza. En el primer caso, en 19 muestras de 20, con seguridad, se encuentra el parámetro que deseamos calcular. De forma complementaria en 1 de 20 muestras no contiene el parámetro deseado, es precisamente este el error que corresponde al 5%. No podemos saber realmente donde esta el parámetro dentro del intervalo, sin embargo, podemos decir con una confianza del 95 % que el intervalo con los limites superior e inferior respectivos contienen el valor real.
Recordemos que la estadística inferencial puede ser de dos tipos:
- Estadística inferencial paramétrica : el requisito es que se debe saber la forma de la distribución de probabilidad que tiene la población que puede ser normal, binomial, Poisson etc.
- Estadística inferencial no paramétrica: no es necesario conocer la distribución de probabilidad de la población.
Los datos de la muestra deben cumplir con ciertos requisitos para que la herramienta estadística pueda ser utilizada adecuadamente, es decir la herramienta sea efectiva.
El intervalo de confianza lo estudiaremos matemáticamente mediante el enfoque paramétrico, es decir haciendo uso de la curva de distribución normal. Durante los siguientes párrafos nos avocaremos a explicar de que forma se calcula el intervalo de confianza como estadístico de una muestra a partir de una población con distribución normal y una muestra completamente aleatoria sin sesgo de muestreo y de medición.
INTERVALO DE CONFIANZA PARA ESTIMAR µ DE UNA POBLACIÓN NORMAL
Verificaremos que el parámetro en estudio pertenezca a una población con distribución normal y la muestra sea aleatoria. Debemos determinar el intervalo de confianza para estimar precisamente la media poblacional (µ).
Si deseamos estimar la media poblacional por el intervalo de confianza, consideraremos los siguientes casos:
CUANDO LA VARIANZA POBLACINAL ES CONOCIDA
Es un caso bastante raro. Generalmente no se conoce la varianza poblacional excepto en casos que se encuentran bajo mucho control de calidad como por ejemplo en la producción de fármacos donde el control de calidad es muy riguroso y la varianza poblacional es conocida.
- Recordemos que
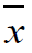 es la media de una muestra de tamaño n mientras que µ es la media poblacional. Es evidente que el estudio parte de los datos estadísticos para llegar a la estimación de los datos poblacionales.
es la media de una muestra de tamaño n mientras que µ es la media poblacional. Es evidente que el estudio parte de los datos estadísticos para llegar a la estimación de los datos poblacionales. - La media muestral de tamaño n se ha obtenido de la muestra a partir de una población con distribución normal. También se considera una muestra aleatoria.
- σ es la desviación estándar poblacional
- Observamos que la coma separa al límite inferior del superior.
Para resolver este tipo de problemas debemos utilizar un programa estadístico donde podemos remplazar los datos.
El soporte probabilístico para construir este
intervalo de confianza es la DISTRIBUCIÓN NORMAL ESTANDARIZADA.
La distribución normal estandarizada
está centrada en cero lo cual quiere decir que su media o esperanza es 0 y su
varianza es 1 N(0,1). Es simétrica. Esto quiere decir que la distribución
normal estandarizada no tiene parámetros, tiene valores fijos 0 y 1 .
La probabilidad o nivel de confianza es una probabilidad
central porque la expectativa de que se encuentre el parámetro se limita en
un lugar central de la gráfica como lo vemos ilustrado más abajo en la campana de Gaus
La distribución de probabilidad normal
estandarizada es soporte para realizar la inferencia mediante IC. Deseamos estimar un parámetro como por ejemplo la media poblacional a partir de un estadístico, en este caso, el intervalo de confianza. Esto equivalente a decir que debemos calcular un intervalo de valores que representa a la media muestral ello nos permite hacer la estimación adecuadamente.
Abajo observamos una gráfica en la que se representa el intervalo de confianza sobre una curva normal estandarizada:
Abajo observamos una gráfica en la que se representa el intervalo de confianza sobre una curva normal estandarizada:
Considerando un error de α=0,05 las áreas extremas son iguales a α/2 por eso decimos que el valor de la abscisa hace referencia a los valores extremos en la gráfica.
Sabemos que la distribución normal estandarizada es
simétrica y esto se representa en la gráfica mediante la curva en forma de
campana donde los valores de la abscisa (desviaciones estándar Z) que se encuentran a la derecha son
iguales pero con signo diferente de los que se encuentran a la izquierda.
Los valores que se presentan en la abscisa de la
distribución normal estandarizada se hallan por cálculos matemáticos pero en
este curso lo haremos con Excel. En los libros de estadista podemos ver las
tablas en donde se hace referencia a los valores (Z) que buscamos en
la distribución normal estandarizada.
Límites de la estimación por intervalos de confianza:
Resolveremos este problema considerando el nivel de
confianza en 0.95, que como ya sabemos es una probabilidad que ocupa una posición central en la gráfica de distribución normal estandarizada. Las áreas extremas
tienen un valor de +-0.025 a la derecha y a la izquierda de la media (0),cuyo
valor en el eje de las abscisas de -1.96 y 1.96 (-+Z1-α/2).
En la figura de arriba observamos la correlación de valores que identifican puntos destacables en la distribución normal estandarizada en donde se considera un error de 5 %. El error máximo tolerable en la distribución es simbolizado por α y es de 0,05 o 5 %, esto quiere decir que los errores acumulados en los extremos es α/2=0,025=2,5%. Una vez establecido el grado de error podemos determinar fácilmente el percentil con el que se relaciona ese valor de probabilidad acumulado en nuestro caso seria 0,975 a la derecha y de 0,025 a la izquierda de la media. el siguiente paso es determinar la desviación estándar (Z) que se corresponde con esos dos percentiles, en nuestro caso sería: -1,96 a la izquierda y 1,96 a la derecha.
Debemos calcular primero la abscisa(desviación estándar) con algunas probabilidades o niveles de confianza, en este caso 0.95 lo cual nos indica un valor de probabilidad aculado extremo igual a +-0.025 que se corresponde a dos valores extremos de desviación estándar Z que indica de forma indirecta la cantidad de valores de la variable aleatoria que se consideran para estimar el parámetro.
Debemos calcular primero la abscisa(desviación estándar) con algunas probabilidades o niveles de confianza, en este caso 0.95 lo cual nos indica un valor de probabilidad aculado extremo igual a +-0.025 que se corresponde a dos valores extremos de desviación estándar Z que indica de forma indirecta la cantidad de valores de la variable aleatoria que se consideran para estimar el parámetro.
En el problema se nos pide calcular la media muestral, ya
tenemos la desviación estándar(9) con estos datos podremos saber cuál intervalo
de confianza.
Resolución:
El promedio según los cálculos en Excel: 6.3056
Con el 95 % de probabilidad se espera que el tiempo(días) promedio poblacional de duración de la enfermedad carbunco tome valores de 5.33 a 7.29 días.
CUANDO LA VARIANZA POBLACIONAL ES DESCONOCIDA
Si deseamos estimar la media muestral de
una muestra aleatoria de tamaño n obtenida de una población normal con variaza
poblacional desconocida entonces:
En este caso el soporte probabilístico ya no es la
distribución normal estandarizada. Por ello el valor ya no es Z sino es t Student
que también es un tipo de distribución para variables aleatorias continuas.
En este caso realizamos
las operaciones con la varianza muestral
y la desviación estándar muestral. Observamos que la varianza muestral ya no
está dividida entre n sino entre n-1 como vemos en la fórmula del gráfico
más arriba.
La distribución T es más o menos parecida a la
distribución normal estandarizada.
También está centrada en cero y es simétrica. La diferencia en reacción a la distribución normal se presenta en la mayor desviación estándar. Tal característica se debe a que la distribución t de Student considera un tamaño de muestra menor y por lo tanto un error estándar mayor. En este modelo de la probabilidad de que las medias muestrales se acerquen a la media poblaciónal es menor que en el modelo de distribución normal. Es por ello que la curva de distribución resulta ser más aplanada, es decir presenta una base más amplia en comparación con la curva de distribución normal. Observaremos que los valores de desviación estándar se corresponden con valores de percentiles más bajos que los que presenta la distribución normal. Esta diferencia se va acartonando a medida que la muestra analizada es mayor a 30 si se incrementa considerablemente la muestra, los valores de percentil y probabilidades son casi idénticos a los de la distribución normal.
Los parámetros de T es : (n-1) como vemos depende del
tamaño de la muestra:
Este tipo de distribución de probabilidad( nos referimos a la forma de distribución en la gráfica en forma de campana mostrada más arriba) es muy buena para hacer inferencias con tamaño de muestras pequeñas. No se recomienda que sean muestras menores de 30 porque los intervalos de confianza se ampliarían demasiado. A medida que la muestra aumenta la distribución Tstuden, como veremos más adelante, se parece a la distribución Z.
En el gráfico de arriba observamos que la probabilidad
de confianza es central, como en el caso anterior de la distribución normal estandarizada, en los extremos se encontrarán las probabilidades α/2
y los valores que delimitan el área de la probabilidad de confianza serán -+T
α/2 que por la simetría tienen el mismo valor pero con signos opuestos.
Observamos que t tiene 35 grados de libertad, recordemos
que esto resulta de (n-1). Además observamos que el análisis se realiza con 95% de
probabilidad de confianza esperado.
Existe una propiedad matemática que indica que cuando
los grados de libertad se incrementan, es decir, el tamaño de la muestra crece
entonces la distribución t student toma la forma de una distribución normal
estandarizada.
La diferencia entre esta distribución y las otras ya
mencionadas se aprecia mejor para muestras pequeñas. El cual tiene un
fundamento estadístico: Con muestra pequeñas las varianza es mayor.
Para resolver este problema debemos calcular primero
la abscisa con algunas probabilidades o niveles de confianza. Se trata de obtener el valor de "t" (desviación estándar) de la
distribución t student. En lo siguiente nos avocaremos a explicar como es que se calculan el valor de "t" en función de los valores de probabilidad error y los grados de libertada en excel:
1
2
3
En los gráficos de arriba las “colas” representan la probabilidad de los eventos con menos y mayor valor (por ejemplo glucemia o colesterol sérico) mientras que en el centro se encuentra los de mayor probabilidad el cual corresponde a valores intermedios de la variable. Cada gráfico presenta dos colas.
Observamos también en el gráfico superior(1) la suma de
las dos colas es 0.10 mientras que en las colas de los dos gráficos que se
encuentran inferiores(2 y 3) la suma es de 0.05.
Pasemos al cálculo de la probabilidad con Excel:
1 valor de t para
probabilidad central igual a: 0.90 con grados de libertada 10
Es importante indicar que si utilizamos la opción DISTR T
entonces estaríamos buscando la probabilidad y para esto tendríamos que tener
el valor de t. En este caso estamos buscando la abscisa y no la
probabilidad por ello vamos a utilizar la DISTRIBUCIÓN T INVERSA:
Al dar siguiente nos sale:
En la imagen de arriba nos están diciendo que la
probabilidad es el valor asociado con la distribución t de student de dos
colas. Para nuestro primer problema es de 0.10. (primera gráfica )
Los grados de libertada en el problema tiene el valor de
10. Con lo cual obtenemos el siguiente resultado:
Resultado:1.812461102
Para hacer el cálculo de los intervalos de confianza
solamente nos falta la varianza muestral o la desviación estándar muetral la
cual se calcula en excel por medio de la opción DESVEST :
Volviendo a la resolución del problema 4 :
Con la formula arriba expuesta:
Con la formula arriba expuesta:
Media:6.3055:
El valor de t: -+1.69
A límite inferior: 6.3055-0.6053=5.70
B límite superior:6.3055+0.6053=6.91
B límite superior:6.3055+0.6053=6.91
Interpretación : con el 95% de probabilidad de confianza
se espera que el tiempo(días) promedio poblacional de la enfermedad de carbunco
tome de 5.70 a 6.91 días. la varianza que se determinó en la investigación fue
de 4.6.
INTEVALO DE CONFIANZA PARA ESTIMAR LA PROPORCIÓN
POBLACIONAL (π) DE UNA POBLACIÓN BINOMIAL
Deseamos calcular el intervalo de confianza para una variable categórica. Anteriormente lo habíamos hecho solamente para variables numéricas, pues este estadístico es propio de variables numéricas. Para lograr un intervalo de confianza de una variable categórica debemos hacer uso de aproximaciones en base a la distribución binomial.
La distribución binomial es de carácter discreto. En este caso π es la probabilidad de éxito. Se usa como soporte probabilística a la distribución normal estandarizada (Z)
La distribución binomial es de carácter discreto. En este caso π es la probabilidad de éxito. Se usa como soporte probabilística a la distribución normal estandarizada (Z)
p: es la proporción muestral
La bondad matemática de este intervalo de confianza para una variable aleatoria DE NATURALEZA CATEGÓRICA con distribución binomial consiste en que si el tamaño de la muestra es grande entonces la probabilidad de éxito está cercana a 0.5 podríamos tener buena aproximaciones a la distribución normal estandarizada. En virtud de esta propiedad matemática vamos a calcular el intervalo de confianza para el parámetro π de una población binomial con la salvedad de que n tiene que ser bien grande en función al tamaño poblacional.
Estimaremos la probabilidad de confianza con 0.90 de probabilidad utilizando la distribución normal estandarizada.
Se espera con un 90 % de probabilidad de confianza que la proporción poblacional de accidentes laborales incapacitantes en esta población tome valores de 11 % a 16 %
Observamos que la interpretación de la proporción poblacional la podemos hacer también en términos de porcentajes.
USO DE LA DESVIACIÓN ESTÁNDAR (DE) Y EL ERROR ESTÁNDAR DE LA MEDIA(EEM) EN EL CÁLCULO DEL INTERVALO DE CONFIANZA (IC)
El uso frecuente del intervalo de confianza en la presentación de los informes de investigación puede conllevar a un mal uso del IC en la interpretación de los datos. El el trabajo clínico generalmente se evalúan múltiples factores para un diagnóstico adecuado. En este sentido es muy útil comparar los valores de una determinada variable medida en el sujeto participante con los valores de referencia indicados el la literatura especializada. El objetivo es supervisar si los valores encontrados de forma particular en un sujeto son semejantes a los que deberían ser dentro de condiciones normales. Para lograr este objetivo clínico debemos realizar una estimación puntual y confeccionar un IC adecuado asociado a la estimación puntual. El problema se presenta cuando interpretamos los valores obtenidos en un sujeto en función de los valores de referencia. Este hecho nos hace considerar la forma de construir nuestro intervalo de confianza. Exinten dos formas de hacer comparaciones según se considere la DE o la EEM en el cálculo IC :
*IC para los datos: en este caso el IC se calcula con la DE y el útil cuando deseamos comparar el valor de una variable medida en un sujeto participante con el rango de toda la población. Este es el caso más frecuente en la práctica clínica.
*IC para la media: en este caso el IC se calcula en el EEM y es útil cuando deseamos comparar la media obtenida en una muestra de investigación con el rango de la distribución muestral en la población total. Este caso se presenta en las investigaciones en donde el propósito es estimar el parámetro de la población.
Para más información les recomendamos leer VARIABILIDAD DE LA MEDICIÓN E INTERVALOS DE CONFIANZA EN LA MEDICINA ¿PORQUÉ DEBERÍAN INTERESARSE LOS RADIÓLOGOS? en la serie de publicaciones radiológicas: Statistical concepts series.















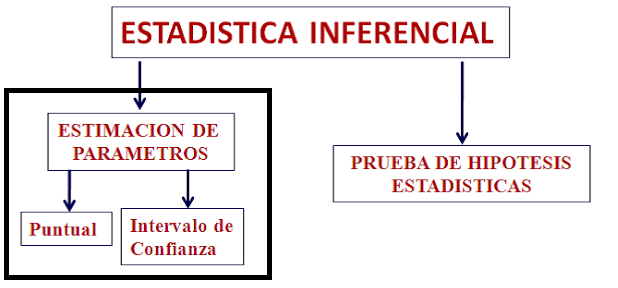








































No hay comentarios:
Publicar un comentario